A Conductor within a Capacitor

[Apteronotus]

Can anyone give me some hints as to how to proceed with the following problem.

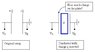
I have a capacitor where one capacitive plate is kept at a potential Va and the other at Vb (grounded). In between the two capacitive plates I insert a conductor which has some charge q on it.

The conductor does not fill the entire space between the two capacitive plates. (See Figure)

If originally the charge on each plate was Q, what is the charge stored on the plates after insertion.

Much thanks

 

[physicsworks]

It depends on how the conductor is placed inside the capacitor and what its width. I'll show you how to calculate the charge on the plates if the conductor has a very small width comparing to other dimensions. Suppose it is placed at the distance L right to the positive (left) plate and has a charge q. Let the distance between the plates be d and in the original setup the charges on the plates are Q and -Q. We want to find the charges q_0 and -q_0 when the conductor is inserted.
Let E_0 be the total electric field due to the plates and E is the electric field due to the conductor. It is obvious that
E_0 = \frac{q_0}{\varepsilon_0 S}
E = \frac{q}{2 \varepsilon_0 S}
where S is an area of the plates and the conductor.
Between the positive (left) plate and the conductor the total field is E_0-E and between the negative (right) plate and the conductor is E_0 + E.
Then we have:
(E_0-E)L + (E_0+E)(d-L)=V_A - V_B \equiv \Delta V
Now inserting in this two above equations for E_0 and E we have:
q_0 = \frac{\varepsilon_0 S}{d} \Delta V - \frac{q(d-2L)}{2d}
or, using the initial conditions
\frac{Q}{\Delta V} = \frac{\varepsilon_0 S}{d} you can rewrite q_0 as:
q_0 = Q - \frac{q(d-2L)}{2d}


OK, now if you have a conductor with non zero width you are doing the same things, just remember that the electric field inside it is zero.

 

[Apteronotus]

Physicsworks, you are a Prince. I am truly grateful. Thank you.