A general formula for the sum of the series 1/k?

[s0ft]

Is there any general expression for the sum to nth term of the series 1/k?

I know that for sufficiently large indices, a good approximation can be ln(b/a) where b and a are the upper and lower limits respectively.
I've tried to do something very simple for the exact sum by constructing unit length rectangles between the curve of the function 1/x and the x axis. This shows clearly that as the values of x gets larger and larger, the integral, being the portion of the rectangle below the curve, gets closer and closer to the actual sum, the total area of the rectangles.

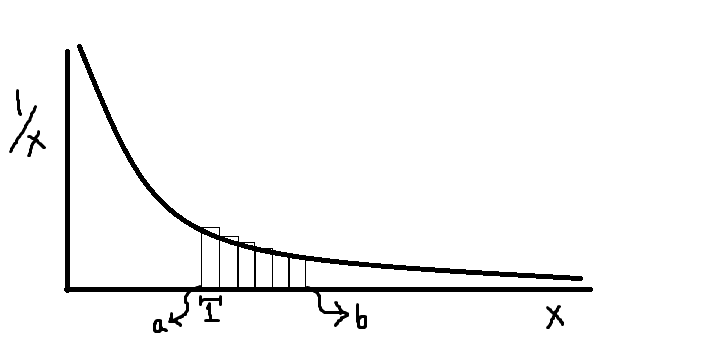
But I don't seem to be able to get any further than this. I did try to account for the extra (above-curve) portions of the rectangles by treating them approximately as triangles(what better option did I have?) and using the 0.5*b*h formula for their area but later realizing that the heights are changing, I thought it wouldn't be so easy.
So, anyone willing to give it a try?

 

[pwsnafu]

See the wikipedia article harmonic number.

 

[s0ft]

I couldn't understand wikipedia pwsnafu. Care to explain?

 

[pwsnafu]

I couldn't understand wikipedia pwsnafu. Care to explain?

Sure. The harmonic numbers are defined $H_n = \sum_{k=1}^n \frac{1}{k}$. Now obviously when you calculate your sum, you'll get a rational number. Fun little fact, the numerators you get (in order) is called the Wolstenholme numbers, and the denominators are called...I don't think they have a name. Hmm.

Anyway, you want to calculate $\sum_{k=a}^b \frac{1}{k}$ when that is $\sum_{k=1}^b \frac{1}{k} - \sum_{k=1}^{a-1} \frac{1}{k} = H_{b}-H_{a-1}$. So that's the answer, you just look them up on the internet and we are done.

But that's not really a satisfactory answer. Now Wikipedia shows two other forms:
$H_n = \int_0^1 \frac{1-x^n}{1-x} dx = \sum_{k=1}^{n}(-1)^k \frac{1}{k} {n \choose k}$.
The first equality is easy: we know
$\frac{1-x^n}{1-x} = \frac{(1-x)(1+x+x^2+\ldots+x^{n-1})}{1-x} = 1+x+x^2+\ldots+x^{n-1}$.
Integrating term by term we get
$x+\frac{x^2}{2}+\frac{x^3}{3} + \ldots + \frac{x^n}{n}$. The terms of the integral is just x=1 and x=0, so we obtain $H_n$.

Follow?

 

[s0ft]

I got lost from the integral for H_n.
Even if I take it as a given, I don't get how it equals the summation part.

 

[pwsnafu]

I got lost from the integral for H_n.
Even if I take it as a given, I don't get how it equals the summation part.

But you do follow what I wrote right?

So moving onto the summation. We want to solve $\int_0^1 \frac{1-x^n}{1-x}dx$.
We do the substitution $u = 1-x$. We get
$\int_0^1 \frac{1-(1-u)^n}{u} du$
if this is not immediately obvious verify it.

Now we expand. You know from the binomial theorem that
$(1-u)^n = 1 - u + {n \choose 2} u^2 - \ldots (-1)^n u^n$
So
$1-(1-u)^n = u - {n \choose 2} u^2 + \ldots (-1)^{n-1} u^n$
And
$\frac{1-(1-u)^n}{u} = 1 - {n \choose 2} u + \ldots (-1)^{n-1} u^{n-1}$

So we calculate
$\int_0^1 1 - {n \choose 2} u + \ldots (-1)^{n-1} u^{n-1} \, du$
is equal to $u - {n \choose 2} \frac{u^2}{2} + \ldots (-1)^{n-1} \frac{u^n}{n} |_0^1$
and we are left with
$1 - {n \choose 2} \frac{1}{2} + \ldots (-1)^{n-1} \frac{1}{n}$
and that's exactly the sum formula.

Edit: 500th post. Yay!

 

[s0ft]

Thank you very much!