Discussion Overview
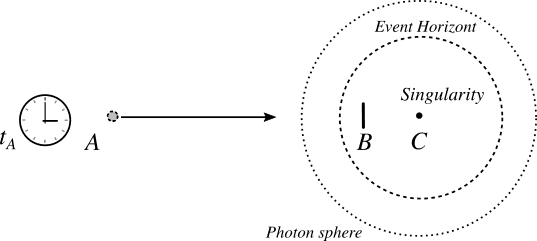
The discussion revolves around a thought experiment involving the placement of a mirror behind the event horizon of a black hole and the implications of turning on a light directed at it. Participants explore concepts related to Schwarzschild spacetime, the nature of singularities, and the behavior of light and objects near the event horizon.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants question the feasibility of placing a mirror behind the event horizon, noting that it cannot remain stationary there.
- There is a contention regarding the depiction of Schwarzschild spacetime, with some arguing that the singularity is not a physical location but rather a moment in the future, suggesting the use of Kruskal diagrams for clarity.
- One participant posits that while light may reflect off the mirror as it falls, the reflected light would also ultimately fall into the singularity.
- Another participant raises a parallel thought experiment about placing a lightbulb behind the event horizon, questioning the difference between reflecting light and simply turning on the light.
- Discussions arise about the nature of singularities in the Schwarzschild solution, with some asserting that the singularity at r = Rs is a result of poor coordinate choice rather than a true singularity.
- Participants express the need to understand the mathematical models used in general relativity to grasp the physical implications of black holes and event horizons.
- There is a debate about the relationship between mathematics and physical reality, with some emphasizing that physics is not about opinions but about understanding the underlying mathematical models.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the implications of placing a mirror behind the event horizon, with multiple competing views on the nature of singularities and the interpretation of Schwarzschild coordinates. The discussion remains unresolved regarding the physical meaning of the mathematical models presented.
Contextual Notes
Participants highlight limitations in understanding the physical implications of mathematical models, particularly in extreme environments like black holes. There are unresolved questions about the nature of singularities and the validity of different coordinate systems used in general relativity.
Who May Find This Useful
This discussion may be of interest to those studying general relativity, black hole physics, or the mathematical foundations of theoretical physics, particularly in understanding the complexities of spacetime and singularities.