A novel way of defining coordinates?

[pervect]

Let's start with the motivation - I'm trying to think of ways to talk about building coordinate systems operationally, ideally without directly using ideas like "space like geodesics" that one needs for fermi-normal coordinates. The ideas behind geodesics don't strike me as terribly complicated, but I get so many virtual blank looks when I mention them that I'd like a different approach.

This is semi-inspired by the large number of people who want to build "frames of reference".

Start by defining a bunch of tiny spheres of constant size - say one wavelength of krypton 86 , 605.78 nanometers. Or perhaps not so tiny, 16508 wavelengths of krypton 86, making them approximately 1cm in size.

We define a sphere as the set of points n wavelengths away from the center.

Close-pack the spheres in a close-centered cubic packing. For "large" spheres, the geometry of space-time would matter, for small enough spheres it shouldn't.

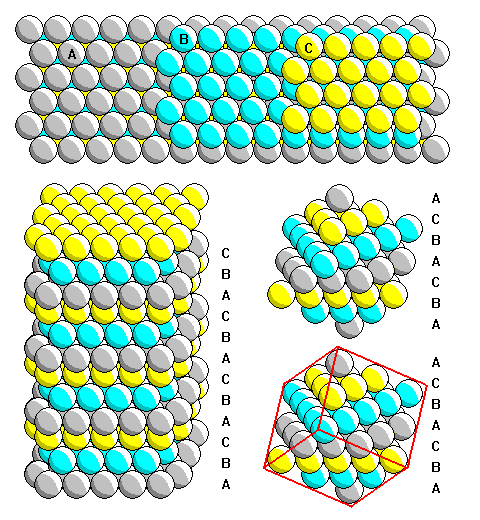
Now imagine that the defining source of krypton 86 is pulsed in short bursts rather than continuous.

The midpoint definition of simultaneity demands that the surface of the spheres all be at the same time, defining a particiular time-slice of space

The cubic packing defines an array of three orthogonal spatial axes.

The constant size of the spheres defines a distance scale.

I would expect that this should be a realization of fermi-normal coordinates, but I' not sure how to prove it.

Also, the scheme seems best suited for static space times, though I suppose you can imagine the construction working for non-static space-times, it's just that the close packed construction wouldn't be static either.

[add]I'm not sure how rigorous and robust the idea of "close packed" really is. Especially if it realizes fermi-normal coordinates - we know that such coordinates are fundamentally limited in size.

But I thought the idea was interesting, and I wonder if there's some refinement that would demonstrate the size limitation.

 

[mfb]

We define a sphere as the set of points n wavelengths away from the center.

n wavelengths in which reference frame?

I wonder how the ideal sphere packing looks like in a spacetime with significant curvature, or even a time-dependent curvature.

 

[DrGreg]

It's difficult to picture this in 3 dimensions, so consider an equivalent construction in 2 dimensions: try paving the surface of the Earth with flat circular tiles. Assume a perfectly spherical Earth and start tiling from one point in a hexagonal pattern where each tile touches six surrounding tiles. Over a small area you won't have a problem, but over a larger area, as the curvature of the Earth's surface becomes non-negligible, you'll find you can't quite fit a tile into the hole formed by 3 of its neighbours, so you'll have to leave a small gap, spoiling the hexagonal construction. The larger the area, the worse this will get -- the cumulative effect of all the small gaps would completely destroy the pattern.

(With a negatively curved surface, the hole formed by neighbouring tiles would be too big, but you'd still have to leave a gap, in a different place.)

 

[pervect]

A good point - I think you might be able to cover the Earth with an array of two slightly different sized circles. I.e. if you make a hexagon of six circles, the inscribed circle will have a different size than the others.

But it's getting complex enough that I think the idea won't really help anyone understand anything.

I think I'd be better off trying to explain the spacelike geodesics as a precurssor towards fermi-normal coordinates.

Though that typicalliy hasn't "gone well" in the past :-(.

 

[sardar]

I find this approach to defining coordinates intriguing and creative. It certainly offers a unique perspective on building coordinate systems without relying on concepts like space-like geodesics. However, it may be challenging to prove that this method is equivalent to fermi-normal coordinates without further investigation and analysis.

One potential limitation of this approach is its reliance on a specific element, krypton 86, which may not be readily available in all situations. Additionally, the use of pulsed bursts instead of continuous sources may also introduce some uncertainties.

I agree that this method may be best suited for static space-times, and further exploration may be needed to determine its applicability to non-static situations. It would also be interesting to explore potential refinements that could address the size limitation and make the approach more robust.

Overall, this is a thought-provoking idea that warrants further investigation and analysis to fully understand its potential and limitations.