student34
- 639
- 21
- TL;DR
- A problem with the solution to the ladder paradox
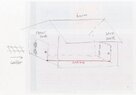
Imagine that there is a very tight string connected to the bottom of each barn door. Each barn door opens and closes vertically. If the string breaks the barn blows up. The doors have to close at the same time for the string not to break. If the doors open one at a time, the extra distance separating the the two doors will surely break the string. Now the ladder goes through at very high speeds. Does the barn explode or not?
It seems as though one of the observers is having an illusion
It seems as though one of the observers is having an illusion