Lajka
- 68
- 0
Hello,
I'm hoping I'm asking this in the right place. If not, I apologize.
Anyway, I have a dilemma about some basics in probabilty and pattern recognition, and, hopefully, someone can help me.
I'm not sure I understand what class-conditional pdf f(x|w_{i}) really means, and it's bothering me. Let me elaborate...
When we use terms such as 'conditional probability pdf and cdf', by that we mean:

where A is some event, a subset of a sample space. This event A must also be the domain of our functions defined above. It's a 'new universe', so to speak, for conditional probability cdfs and pdfs, and they only make sense if we look at them over this event A. For example, if we look at the random variable X with Gaussian distribution, and we denote event A as A={1.5<X<4.5}, then the corresponding conditional probability functions (pdf & cdf) look like
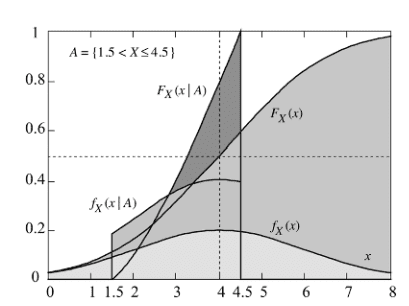
As you can see, they're defined only over interval {1.5<x<4.5}, otherwise they wouldn't make sense.
Often we are interested in conditional probabilites functions where the event A = (Y=y_{0}), and then we have
f(x|y)= f(x|Y=y_{0})=f(x,y_{0})/f_{Y}(y_{0})
We can interpret function f(x|y) as an intersection of a joint pdf f(x,y) with a plane y=y_{0} (with f_{Y}(y_{0}) as a normalization factor).
This is all fairly basic stuff, I reckon. And these types of conditional probability functions are the only types I know that exist, and they're all defined over region which is the event which serves as a condition (I can't stress this enough, for reasons seen later). But class-conditional probability functions, such as f(x|w_{i}) in Bayes classifiers theory, seem like a different beast to me.
First of all, let me say that everything about these conditional pdfs, and naive Bayes classifier in general, is perfectly intuitive to me and I don't have a problem from that POV. I understand that, and I don't have the problem with the logic itself presented here. But when I try to define everything rigorously from a mathematical POV, I get stuck.
In other words, I understand what p(x|w_{i}) represents, and why, for instance, p(x|w_{1}) is non-zero even over region w_{2}. However, I don't know how to explain all that using rigorous mathematical apparatus. Let me elaborate even more...
So, we have these classes w_{i}. What exactly are they, mathematically speaking?! Their priors sum up to one, and they will eventually be represented by regions in our sample space, so I will define them as events in my sample space. If we look at the simplest example in 1-D, the conditional probability density functions would look something like this
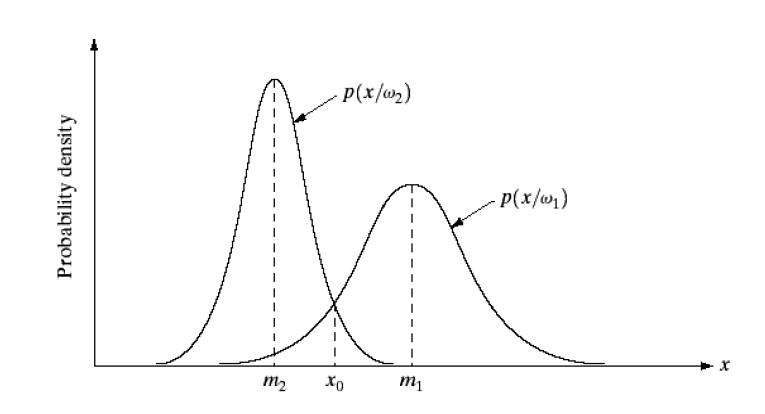
And then we could tell that event w_{1} is (-inf, \, x_{0}) and event w_{2} is (x_{0},\, +inf).
If you ask me, this doesn't make sense if you consider the definitions of conditional pdfs above. Conditional probability density function, by its very definition, must be confined to a space of the event it's conditioned with. In other words, p(x|w_{1}) should be constrained to the w_{1} region! But not only that it isn't, it spreads out over the w_{2} region as well! That shouldn't be possible, because w_{1} and w_{2} are mutually exclusive events, and their respective regions also do not overlap, which makes sense. But conditional probability density functions defined over them do? Wait, what?!
Of course, this is how we define the error of our classification, but all this doesn't look very convincing to me, strictly mathematically speaking.
Conditional pdf p(x|A) must be defined over the region which corresponds to the event A, period. Functions p(x|w_{1}) and p(x|w_{2}) shouldn't overlap each other like that, because the regions w_{1} and w_{2} are mutually exclusive. This is what basic theory of conditional probability density functions tells us.
So, this is why I think that p(x|w_{i}) is not an ordinary conditional pdf like the one defined in the beginning of this post. But what is it then?! I don't know, I'm confused. Or maybe I shouldn't interpret classes w_{i} as regions in the sample space, and that's the mistake I'm making here. But what are they then, how should I interpret them?
Also, if I assume that it's okay to interpret classes w_{i} as as regions in space, isn't there a recursive problem, because we first define p(x|w_{i}) over, supposedly known, event w_{i}, but we actually don't know what region the event w_{i} occupies in sample space? Because, that's, like, the point of classification, to determine these regions, that's what this is all about.
But is this really okay, to define a function in the beginning which domain is actually unknown?
Hopefully, I made at least some sense here, and thanks in advance for any help I can get.
Cheers.
I'm hoping I'm asking this in the right place. If not, I apologize.
Anyway, I have a dilemma about some basics in probabilty and pattern recognition, and, hopefully, someone can help me.
I'm not sure I understand what class-conditional pdf f(x|w_{i}) really means, and it's bothering me. Let me elaborate...
When we use terms such as 'conditional probability pdf and cdf', by that we mean:
where A is some event, a subset of a sample space. This event A must also be the domain of our functions defined above. It's a 'new universe', so to speak, for conditional probability cdfs and pdfs, and they only make sense if we look at them over this event A. For example, if we look at the random variable X with Gaussian distribution, and we denote event A as A={1.5<X<4.5}, then the corresponding conditional probability functions (pdf & cdf) look like
As you can see, they're defined only over interval {1.5<x<4.5}, otherwise they wouldn't make sense.
Often we are interested in conditional probabilites functions where the event A = (Y=y_{0}), and then we have
f(x|y)= f(x|Y=y_{0})=f(x,y_{0})/f_{Y}(y_{0})
We can interpret function f(x|y) as an intersection of a joint pdf f(x,y) with a plane y=y_{0} (with f_{Y}(y_{0}) as a normalization factor).
This is all fairly basic stuff, I reckon. And these types of conditional probability functions are the only types I know that exist, and they're all defined over region which is the event which serves as a condition (I can't stress this enough, for reasons seen later). But class-conditional probability functions, such as f(x|w_{i}) in Bayes classifiers theory, seem like a different beast to me.
First of all, let me say that everything about these conditional pdfs, and naive Bayes classifier in general, is perfectly intuitive to me and I don't have a problem from that POV. I understand that, and I don't have the problem with the logic itself presented here. But when I try to define everything rigorously from a mathematical POV, I get stuck.
In other words, I understand what p(x|w_{i}) represents, and why, for instance, p(x|w_{1}) is non-zero even over region w_{2}. However, I don't know how to explain all that using rigorous mathematical apparatus. Let me elaborate even more...
So, we have these classes w_{i}. What exactly are they, mathematically speaking?! Their priors sum up to one, and they will eventually be represented by regions in our sample space, so I will define them as events in my sample space. If we look at the simplest example in 1-D, the conditional probability density functions would look something like this
And then we could tell that event w_{1} is (-inf, \, x_{0}) and event w_{2} is (x_{0},\, +inf).
If you ask me, this doesn't make sense if you consider the definitions of conditional pdfs above. Conditional probability density function, by its very definition, must be confined to a space of the event it's conditioned with. In other words, p(x|w_{1}) should be constrained to the w_{1} region! But not only that it isn't, it spreads out over the w_{2} region as well! That shouldn't be possible, because w_{1} and w_{2} are mutually exclusive events, and their respective regions also do not overlap, which makes sense. But conditional probability density functions defined over them do? Wait, what?!
Of course, this is how we define the error of our classification, but all this doesn't look very convincing to me, strictly mathematically speaking.
Conditional pdf p(x|A) must be defined over the region which corresponds to the event A, period. Functions p(x|w_{1}) and p(x|w_{2}) shouldn't overlap each other like that, because the regions w_{1} and w_{2} are mutually exclusive. This is what basic theory of conditional probability density functions tells us.
So, this is why I think that p(x|w_{i}) is not an ordinary conditional pdf like the one defined in the beginning of this post. But what is it then?! I don't know, I'm confused. Or maybe I shouldn't interpret classes w_{i} as regions in the sample space, and that's the mistake I'm making here. But what are they then, how should I interpret them?
Also, if I assume that it's okay to interpret classes w_{i} as as regions in space, isn't there a recursive problem, because we first define p(x|w_{i}) over, supposedly known, event w_{i}, but we actually don't know what region the event w_{i} occupies in sample space? Because, that's, like, the point of classification, to determine these regions, that's what this is all about.
But is this really okay, to define a function in the beginning which domain is actually unknown?
Hopefully, I made at least some sense here, and thanks in advance for any help I can get.
Cheers.