A seemingly easy logical question

  • Thread starter maverick_bih
  • Start date
In summary, the goal of this task is to connect all three circles to each of the three triangles without any lines crossing. However, it is impossible to do so as there will always be a separated area on each side of the lines connecting the circles and triangles. This can be seen in the attached gif or by visualizing it on the surface of a torus.
  • #1
maverick_bih
1
0
This looks like an easy one, but I haven't found anyone yet who has answered it correctly, including me...
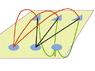
So, the goal is (like shown in the picture), to connect all three circles to each of the three triangles (nine connections in total, i have managed eight). Give it a try. You can go around the triangles and circles with the lines, just as long as they DON'T cross.

∆ ∆ ∆

O O O
 
Last edited:
Physics news on Phys.org
  • #2
What picture?
 
  • #3
It's impossible. Let's call the triangles T1, T2, T3 and the circles C1, C2, C3. There will be a separated area on each side of the lines going from T1 to C1 to T2 to C2. Let's call one of these areas Ž and the other Đ. There will also be a line going from C1 to T3 to C2, subdividing one of the areas, let's say Đ, into two new areas, one touching T1 which we will call Æ and one touching T2 which we will call Ø, giving a total of three separated areas. T3 now neighbours areas Æ and Ø, T1 neighbours Ž and Æ and T2 neighbours Ž and Ø. No matter which of these areas C3 is in, only one of the points T1, T2 and T3 will be on the edge of this area.
 
  • #4
See attached gif.
 

Attachments

  • Connect6.gif
    Connect6.gif
    7.6 KB · Views: 473
  • #5
Martin Rattigan said:
See attached gif.

You could also do it in "two dimensions" on the surface of a torus (donut).
 

1. What is "A seemingly easy logical question"?

"A seemingly easy logical question" is a phrase often used to describe a question that appears simple on the surface, but requires critical thinking and logical reasoning to answer correctly. It may involve complex concepts or require a deeper understanding of a subject.

2. Why are seemingly easy logical questions important?

Seemingly easy logical questions are important because they challenge our thinking and problem-solving skills. They help us develop critical thinking abilities and improve our understanding of complex concepts. They also allow us to approach problems from different perspectives and find creative solutions.

3. How can I improve my ability to answer seemingly easy logical questions?

There are several ways to improve your ability to answer seemingly easy logical questions. These include practicing regularly, developing your critical thinking skills, and staying curious and open-minded. It can also be helpful to break down the question into smaller parts and analyze each component separately.

4. Can seemingly easy logical questions have more than one correct answer?

Yes, seemingly easy logical questions can have multiple correct answers. This is because they often involve complex concepts and there can be different ways to approach and solve the problem. However, it is important to provide a logical and well-supported answer, rather than just guessing or providing any random answer.

5. How can I use seemingly easy logical questions in my research or experiments?

Seemingly easy logical questions can be used in research or experiments to test hypotheses, identify and solve problems, and generate new ideas. They can also help to uncover underlying assumptions and biases, leading to more accurate and comprehensive findings. Additionally, they can be used to evaluate the validity and reliability of data and results.

Similar threads

B Traditional logic and its usefulness in the past
    • Set Theory, Logic, Probability, Statistics
Replies
21
Views
2K
A Recalculate a range by variable 'Median'?
    • Set Theory, Logic, Probability, Statistics
Replies
4
Views
727
I Three inertial particles: Separating the twins from the paradox
    • Special and General Relativity
2
Replies
40
Views
2K
In Search of: Cheap/common pressure switch
    • General Engineering
Replies
17
Views
2K
A Three generations of Fermions from octonions Clifford alegbras
    • Beyond the Standard Models
2
Replies
61
Views
6K
Electronics Switches, Pots, Displays for DIY projects - Some ideas, some questions
    • DIY Projects
Replies
6
Views
2K
Deriving the Law of Reflection from Huygens Principle
    • Optics
Replies
5
Views
1K
B Is the Geometry/Topology of Mazes a thing?
    • General Math
Replies
18
Views
1K
CRT gun "dissection" questions
    • Electrical Engineering
Replies
12
Views
1K
Can an object maintain uniform motion without any external force?
    • Mechanics
2
Replies
66
Views
3K

Hot Threads

Recent Insights

Back
Top