Undergrad How Does the Ratio Test Determine Convergence in Power Series?

[Leo Liu]

TL;DR

{$A_n$} is a sequence of positive numbers. $\sum_{n=0}^{\infty} A_n(x-1)^n$ has a R of convergence $R=\frac 3 2$. Does $\sum_{n=0}^{\infty} A_n$ converge or diverge?

I tried to use the ratio test, but I am stuck on finding the range of the limit.
$$\because \left|x-1\right|<1.5=Radius$$
$$\therefore -0.5<x<2.5$$

$$\lim _{n \to \infty} \left| \frac{A_{n+1}(x-1)^{n+1}}{A_n(x-1)^n} \right|$$
$$\lim_{n \to \infty} \frac{A_{n+1} \left|x-1\right|}{A_n} <1$$
$$\lim_{n \to \infty} \left| \frac{A_{n+1}}{A_n} \right|< \frac 1 {\left| x-1 \right|}$$

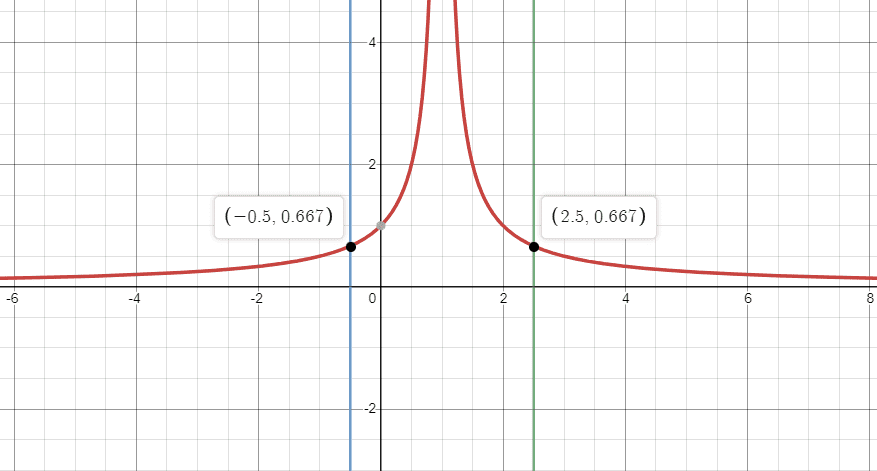
Then I plotted the graph of 1/|x-1| and I found that the limit of A_n+1/A_n could vary from 2/3 (convergent) to infinity (divergent), as shown by the image below. What should I do next?

 

[PeroK]

What happens if you take $x = 2$?

 

[Leo Liu]

What happens if you take $x = 2$?

No conclusion?

 

[PeroK]

No conclusion?

What does that mean? Is $2$ inside or outside the radius?

 

[Leo Liu]

What does that mean? Is $2$ inside or outside the radius?

Does this show the radius of convergence $R'$ of the series A_n is 2?

 

[PeroK]

It means we have to use another method to test the convergence of the series. 2 is in the radius R.

Eh?

Summary:: {$A_n$} is a sequence of positive numbers. $\sum_{n=0}^{\infty} A_n(x-1)^n$ has a R of convergence $R=\frac 3 2$.

 

[Leo Liu]

Eh?

I think it is in the radius of convergence because $-0.5<2<2.5$

 

[PeroK]

I think it is in the radius of convergence.

You're saying that you think $2 < \frac 3 2$?

 

[Leo Liu]

You're saying that you think $2 < \frac 3 2$?

No, but I am quite confused--we are talking about x, not $\left| x-1 \right|$, right?

 

[PeroK]

No, but I am quite confused--we are talking about x, not $\left| x-1 \right|$, right?

Yes, sorry, of course it's inside the radius of convergence. In any case, what does $x = 2$ tell you about $A_n$?

 

[Leo Liu]

You're saying that you think $2 < \frac 3 2$?

Can you please tell me what I should do next? This is not a homework question and I am doing it just for interest.

 

[PeroK]

Can you please tell me what I should do next? This is not a homework question and I am doing it just for interest.

I've actually told you: put $x = 2$.

 

[Leo Liu]

Yes, sorry, of course it's inside the radius of convergence. In any case, what does $x = 2$ tell you about $A_n$?

When $x \geq 2 \: or \: x \leq 0$, the series converges.

 

[PeroK]

When $x>2 \: or \: x<0$, the series converges.

And what is the series when $x = 2$?

 

[Leo Liu]

And what is the series when $x = 2$?

Converges at x=2?

 

[PeroK]

Converges at x=2?

Write down the sequence for $x = 2$.

 

[Leo Liu]

Write down the sequence for $x = 2$.

$$\sum_{n=0}^ \infty{A_n}$$

 

[PeroK]

$$\sum_{n=0}^ \infty{A_n}$$

That's what you should have done after post #2.

 

[Leo Liu]

That's what you should have done after post #2.

Oh, thank you! So it is actually convergent because the limit is less than 1 if we sub in x=2!

 

[PeroK]

Oh, thank you! So it is actually convergent because the limit is less than 1 if we sub in x=2!

In general, the series:
$$\sum_{n = 0}^{\infty} A_n $$
converges, if and only if the power series:
$$\sum_{n = 0}^{\infty} A_n x^n$$
converges at $x = 1$.

Those two properties are clearly equivalent.