conectado
- 1
- 0
Hey I either have the worst physics textbook in the history of physics textbooks or i can't understand a topic.I'd appreciate if you help me decide which is it.
(Pic related is the image of the example)
First let's agree on the symbols let's call angular velocity: \omega = \frac{rxv}{||r||^2} , angular momentum L=rxmv and Lineal Momentum:P=mv. Being that defined, the book attemps to proof that L and [math]\omega[/math] have generally different directions, here is the first problem i encountered, for what i know m||r||^2\omega = L being m||r||^2 That means that Angular Velocity and Angular Momentum are parallel therefore have the same direction, the example proceed as following: 2 puntual mass are united by a rigid bar of despicable mass, therefore both have the same angular momentum. the momentum of body 1 is L_1 = r_1xm_1v_1 and it explicitly say that it's easy to see that it's contained in the plane given by P_1 P_2 \omega (which i fail to see) being the direction perpendiculat to the line that unites P_1 with P_2 and that L_2 Has the same direction that L_1. Therefore the Angular Impulse make an angle of \frac{\pi}{2}-\alpha with the axis of rotation(\omega). Well that'd be an example i'd really appreciate if someone can clarify my doubts, i don't have a teacher to ask since i study by my own.
Here is a picture of the example:
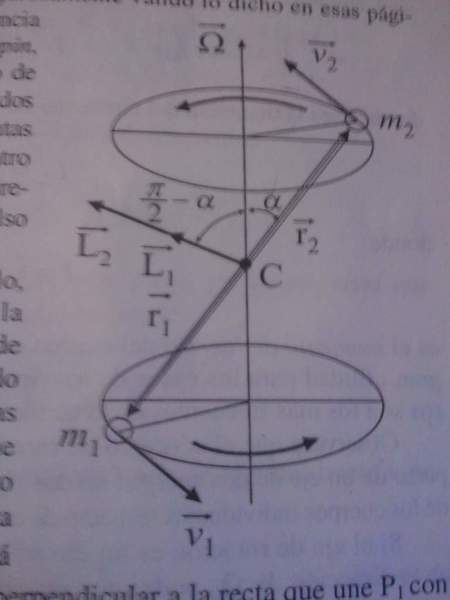
(Pic related is the image of the example)
First let's agree on the symbols let's call angular velocity: \omega = \frac{rxv}{||r||^2} , angular momentum L=rxmv and Lineal Momentum:P=mv. Being that defined, the book attemps to proof that L and [math]\omega[/math] have generally different directions, here is the first problem i encountered, for what i know m||r||^2\omega = L being m||r||^2 That means that Angular Velocity and Angular Momentum are parallel therefore have the same direction, the example proceed as following: 2 puntual mass are united by a rigid bar of despicable mass, therefore both have the same angular momentum. the momentum of body 1 is L_1 = r_1xm_1v_1 and it explicitly say that it's easy to see that it's contained in the plane given by P_1 P_2 \omega (which i fail to see) being the direction perpendiculat to the line that unites P_1 with P_2 and that L_2 Has the same direction that L_1. Therefore the Angular Impulse make an angle of \frac{\pi}{2}-\alpha with the axis of rotation(\omega). Well that'd be an example i'd really appreciate if someone can clarify my doubts, i don't have a teacher to ask since i study by my own.
Here is a picture of the example:
Last edited: