About Work done when velocity is constant

[Iwanttolearnphysics]

Homework Statement

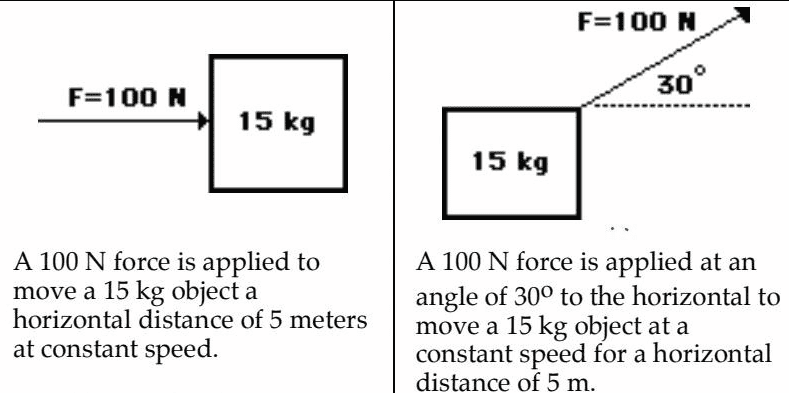
Question 1: A 100N force is applied to move a 15kg object a horizontal distance of 5 meters at constant speed.
Question 2: A 100N force is applied at an angle of 30degrees to the horizontal to move a 15kg object at a constant speed for a horizontal distance of 5m.

Relevant Equations

Fnet = ma
W = Fs

Here's where I got the questions:

• These are from a worksheet I downloaded online: Answer Key
• The answer key says that the answer to the first question is 500J and for the next question it's 433J.
• It says constant speed though, so I don't understand why the answers aren't zero. I get how they got 500J and 433J since it's just basic math, but this doesn't make any sense to me conceptually.
• How can work be done when acceleration is zero?
• What do I not understand? Please help me out.

EDIT:

• I get it now. Nevermind! It says on the key that it's the "work done by the applied force" not the net force.
• Still though, is my understanding correct, that if there's no acceleration, there's no net work?

 

[Lnewqban]

Why do you link acceleration and work?

 

[Iwanttolearnphysics]

Why do you link acceleration and work?

Because work is equal to force times displacement, and force is equal to mass times acceleration. If there's no acceleration, there's no net force. If no net force, no work is done. No?

 

[kuruman]

In this case, your system is a single block. For it to move at constant speed under the influence of a non-zero force, there must be at least one additional non-zero force acting on the block to make the net force, and hence the acceleration, zero. If you define the net work as the sum of the works done by all the forces on the block, then the net work is zero. You can write
$$W_{\text{net}}=\sum_i W_i=\sum_i \left(\vec F_i\cdot \vec s\right)=\left(\sum_i \vec F_i\right)\cdot \vec s=\vec F_{\text{net}}\cdot\vec s={m~ \vec a\cdot \vec s}$$When the acceleration is zero, the net work is zero.

 

[Iwanttolearnphysics]

In this case, your system is a single block. For it to move at constant speed under the influence of a non-zero force, there must be at least one additional non-zero force acting on the block to make the net force, and hence the acceleration, zero. If you define the net work as the sum of the works done by all the forces on the block, then the net work is zero. You can write
$$W_{\text{net}}=\sum_i W_i=\sum_i \left(\vec F_i\cdot \vec s\right)=\left(\sum_i \vec F_i\right)\cdot \vec s=\vec F_{\text{net}}\cdot\vec s={m~ \vec a\cdot \vec s}$$When the acceleration is zero, the net work is zero.

Thank you! I guess I understand it then. I just wanted to make sure.

 

[PeroK]

Because work is equal to force times displacement, and force is equal to mass times acceleration. If there's no acceleration, there's no net force. If no net force, no work is done. No?

Yes, but it's a common practical situation to be doing work and applying a force only to maintain constant velocity. That would apply to a car, bicycle, pulling a sledge or any sort of machinery that has reached its constant running speed: the engine must do work to maintain that constant speed - owing to the inevitability of forces of resistance.

 

[LastScattered1090]

• Still though, is my understanding correct, that if there's no acceleration, there's no net work?

Sort of yes. I'd phrase it a bit differently. If there is no acceleration, then by Newton's Second Law, there must be no net force. All the individual forces acting on the object can still do work, but the total work done by them must sum to zero. Correspondingly, there is no change in the kinetic energy of the body.

 

[Iwanttolearnphysics]

Yes, but it's a common practical situation to be doing work and applying a force only to maintain constant velocity. That would apply to a car, bicycle, pulling a sledge or any sort of machinery that has reached its constant running speed: the engine must do work to maintain that constant speed - owing to the inevitability of forces of resistance.

Yeah, that makes sense. I was just about to ask something like that but you beat me to it. Thank you.

 

[Iwanttolearnphysics]

Sort of yes. I'd phrase it a bit differently. If there is no acceleration, then by Newton's Second Law, there must be no net force. All the individual forces acting on the object can still do work, but the total work done by them must sum to zero. Correspondingly, there is no change in the kinetic energy of the body.

If the total work done is zero, doesn't that mean that the net work done is zero? I don't understand how those are different. Is it just semantics that I say the net force done is zero, so the total work done must equal to zero? Or can I use net work? Thank you!

 

[kuruman]

If the total work done is zero, doesn't that mean that the net work done is zero? I don't understand how those are different. Is it just semantics that I say the net force done is zero, so the total work done must equal to zero? Or can I use net work? Thank you!

What, in your mind, is the difference between total work and net work done on the block of this example? Please explain in your own words or with equations.

 

[Iwanttolearnphysics]

What, in your mind, is the difference between total work and net work done on the block of this example? Please explain in your own words or with equations.

Okay. I think I get it now. They're different. Net work is the vector sum of all the work done by all the forces acting on an object. Total work, I guess, is the sum of all the absolute values of work done by all the forces acting on an object. If what I said is correct, then would it also be correct to say that one is scalar and the other is a vector? Thanks.

 

[jbriggs444]

@kuruman asks about the definitions in your mind for net work and for total work.

Part of his point is that terminology is secondary. Understanding is the important thing. We want to make sure that we are talking about the same things. Whether we call it "net work", "total work" or "center of mass work".

Net work is the vector sum of all the work done by all the forces acting on an object.

Work, like energy, is a scalar. One does not take the vector sum of a scalar.

For a rigid, non-rotating object the displacement of all of the object's components will match the displacement of the object as a whole. $(\sum F_i) \cdot ds = \sum (F_i \cdot ds)$. So for rigid, non-rotating objects, we do not have to be careful about whether we add up the forces first and then multiply by the displacement to get net work of whether we multiply the individual forces by the individual displacements and then add to get net work.

For non-rigid or rotating objects, one does need to track the individual forces and the individual displacements. One can have a zero net force while still performing non-zero total work. For instance, compressing a spring with equal and opposite forces on the two ends or spinning a wheel by applying a force "couple".

 

[Iwanttolearnphysics]

@kuruman asks about the definitions in your mind for net work and for total work.

Part of his point is that terminology is secondary. Understanding is the important thing. We want to make sure that we are talking about the same things. Whether we call it "net work", "total work" or "center of mass work".Work, like energy, is a scalar. One does not take the vector sum of a scalar.

For a rigid, non-rotating object the displacement of all of the object's components will match the displacement of the object as a whole. $(\sum F_i) \cdot ds = \sum (F_i \cdot ds)$. So for rigid, non-rotating objects, we do not have to be careful about whether we add up the forces first and then multiply by the displacement to get net work of whether we multiply the individual forces by the individual displacements and then add to get net work.

For non-rigid or rotating objects, one does need to track the individual forces and the individual displacements. One can have a zero net force while still performing non-zero total work. For instance, compressing a spring with equal and opposite forces on the two ends or spinning a wheel by applying a force "couple".

Thank you! I appreciate the detailed explanation.