Acceleration and tension of pulley system

[Fizic]

Honestly I'm not sure if I've made any mistakes here, but I've been having considerable difficulty with tension problems. This is also the first pulley problem I've attempted, so I'm sure I've made a blunder or two somewhere. If someone could review what I've done so far that would be very helpful.

Problem Text:

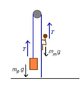
A 10kg monkey climbs up a massless rope that runs over a frictionless tree limb and back down to a 15kg package on the ground.

A)What is the magnitude of the least acceleration the monkey must have if it is to lift the package off the ground? If, after the package has been lifted the monkey stops climbing and hold onto the rope, what are

B)The magnitude and

C) Direction of the monkey's acceleration, and

D) What is the tension on the rope?

The figure given looks something like this.
_____
|LIMB|
|...|
|...|
|...|
|...|
[M] [P]

M_M=10kg
M_P=15kg

What I've done

A) The monkey, at rest, pulls on the rope with a downward force of 10kg$\bullet$9.8m/s²=98N

The package pulls on the rope 15kg$\bullet$9.8m/s²=147N

To put the package in motion, a net force has to be applied (i.e. the monkey cancels out the normal force). I take this to mean that the monkey must apply a downward force of at least 147N-98N=49N.

To create a force of downward force of 49N, the 10kg monkey must climb upwards at $\frac{49N}{10kg}$=4.9m/s².

B) When the monkey stops climbing, the only forces are 147N and 98N by the package and monkey respectively.

The net force will be 49 N downwards on the package side.

The acceleration will therefore be $\frac{49N}{10kg+15kg}$=1.96m/s²

C) Up

D) F_net=1.96m/s$\bullet$15kg=29.4N

F_tension=F_gravity-F_net

=147N-29.5N

=117.6N

 

[ehild]

Your solution is correct. Nice work!

In case of such pulley-rope-tension problems you assume that the rope has no mass (unless it stated otherwise). If there is no other force acting on the rope but those at the end , these forces must be equal. The rope pulls back at the same force: that is called tension, and the tension is the same all along the rope.

With two bodies hanging on the rope draw a Free-Body Diagram (FBD) showing the forces exerted on both bodies. See attachment.

There is gravity downward and tension upward both for the package and the monkey. The net force =ma.

For the package: T-m_pg=ma_p
For the monkey: T-m_mg=ma_m

The package just starts to accelerate, a_p≥0, so T-m_pg≥0. Choose a_p=0, T=m_pg, substitute for T and solve for a_m.

When the monkey does not climb any more, the length of the rope does not change. The package will descend the same distance as the monkey raises: a_p=-a_m. Solve the system of equation with that condition.

ehild