Acceleration and velocity of a mass attached to a sphere

[JulienB]

Homework Statement

Hi everybody! Still checking my comprehension of physics, and hopefully those posts will help other users!

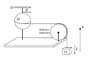
A homogeneous wooden sphere with mass M and radius R rotates about a perpendicular axis going through its center of mass. At the top of this axis is a homogeneous metal bar of length 2R and of same mass M. A massless string is rolled around the ball (see attached picture) and on its other end goes through a wheel and has a suspended mass attached to it. There is no friction.
a) calculate the moment of inertia of the system wooden ball-metal bar regarding its rotation axis. The bar should be considered as infinitely thin. The moment of inertia of a sphere is J_K = (2/5)MR².
b) what is the acceleration of the mass m in the field of gravity of Earth?
c) what is the velocity of the mass m when it has gone down a distance h?

Homework Equations

Moment of inertia, torque, Newton 2nd and 3rd laws, conservation of energy

The Attempt at a Solution

Though it is not the hardest problem, I find the calculations messy and the risk of missing something high. Here is what I've done:

a) First I calculate the moment of inertia of the bar:

J_S = (1/12)M(2R)² = ⅓⋅MR²
⇒ J_total = (2/5 + ⅓)MR² = (11/15)MR²

Im pretty sure I can add the moments of inertia that way since they have the same axis of rotation, right?

b) By Newton's 3rd law I know that the force of tension of the string on the mass is equal to the force of tension of the string on the sphere. I try to find an expression for T using the torque and the angular acceleration:

Στ = T⋅R
⇒ α = Στ/J = 15T/11M

The angular acceleration is also equal to tangential acceleration/radius a_T/R, and in that case a_T = a (the acceleration of the suspended mass):

⇒15T/11M = a/R ⇒ T = 11aR/15M

I plug that into the Newton's 2nd law:

a = ΣF/m = g - 11a⋅m⋅R/15M
⇒ a = g/(1 + 11m⋅R/15M)

c) For that part I set up an equation of conservation of energy. I assume that the system starts at rest:

m⋅g⋅h = ½⋅m⋅v² + ½⋅J⋅ω²

Is that correct? I have a little doubt about the rotational energy.

Then I substitute ω by v/R. Here again I have a little doubt: I allow myself this substitution because I think the velocity of the string at the sphere should be the same as the velocity at the mass. Anyway that gives me for the velocity:

v = √(2⋅m⋅g⋅h/(m + 11M/15))

What do you guys think? It's always a bit tricky not to misjudge such a situation..Thank you in advance for your answers!Julien.

 

[TSny]

J_S = (1/12)M(2R)² = ⅓⋅MR²
⇒ J_total = (2/5 + ⅓)MR² = (11/15)MR²

Im pretty sure I can add the moments of inertia that way since they have the same axis of rotation, right?

Yes. J_total looks good.

b) By Newton's 3rd law I know that the force of tension of the string on the mass is equal to the force of tension of the string on the sphere. I try to find an expression for T using the torque and the angular acceleration:

Στ = T⋅R
⇒ α = Στ/J = 15T/11M

If you mean M to be in the denominator, then you should use parentheses: 15T/(11M). However, this expression is not correct as you can tell by the dimensions. Did you get all the factors of R taken care of?

a = g/(1 + 11m⋅R/15M)

Again, you can check the dimensions of the last term in parentheses and see that this cannot be correct. Is little m equal to big M? If so, you can simplify.

Your work for (c) looks good to me. Again, you can simplify if m = M. You can also check whether or not the answer for (c) is consistent with (b) by using the acceleration to find the final v.

 

[JulienB]

If you mean M to be in the denominator, then you should use parentheses: 15T/(11M). However, this expression is not correct as you can tell by the dimensions. Did you get all the factors of R taken care of?

Again, you can check the dimensions of the last term in parentheses and see that this cannot be correct. Is little m equal to big M? If so, you can simplify.

@TSny Thank you for your answer. I've reviewed the calculations and I indeed forgot a factor R. I now get T = (11/15)a⋅M and therefore a = g/(1 + 11M/(15m)). I believe the units are consistent this time.

Unfortunately as far as I know m ≠ M, so I cannot simplify any further, but the R I forgot already simplified the expression a little bit since it does not depend on it anymore.Julien.

 

[TSny]

OK. Your answers look right to me. You can check some limits to see if it makes sense. If M goes to zero, what is a? If M goes to infinity, what is a? If m goes to zero, what is a? If m goes to infinity, what is a?

 

[JulienB]

@TSny thanks I'm always fond of ways to check the consistency of an answer!

- if M goes to 0, then the acceleration is g. Makes sense since the mass m would not be held back by anything then.
- if M goes to infinity, the acceleration goes to 0. Makes also sense since m would then be held back by a much heavier mass.
- if m goes to 0, the acceleration also goes to 0. There is no more mass on which to apply the force of gravity,
- if m goes to infinity, a also goes to infinity. The force of gravity being applied onto an infinitely heavy mass, that also makes sense.

That's great! I will make sure I use those instinctive methods of verification during my exams!Julien.

 

[TSny]

Great!