Wooden sphere rolling on a double metal track

[Hak]

Homework Statement

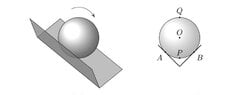
Two rectangular pieces of metal are joined at right angles, forming a guide with two surfaces, which is then tilted at an angle $\alpha$ . A wooden ball descends down the rail, rolling without sliding. The figure shows the image from the side, and then from the front, viewed from below.

1.) Which point on the surface of the sphere has maximum instantaneous velocity?
2.) If $v$ is the speed at which the sphere falls, what speed does that point have?
3.) What is the minimum value of the coefficient of static friction between metal and wood?

Figure: https://imgur.com/tWy7d2n

edit: {See included figure at bottom}

Relevant Equations

/

About points 1. and 2., I assumed that the point of the sphere moving with maximum velocity is $Q$ and that the velocity at that point is $v_Q= 2v$. In fact, at the highest point of a rotating sphere, the velocity is given by the sum of the velocities of translation and rotation. Since, in a pure rolling condition, the two velocities are equal, then the velocity at $Q$ will be:
$$v_Q = v + v = 2v$$

About point 3. I drew a sketch including the normal force, components of the weight, and the static friction force. There is barely enough
friction to keep the cylinder rolling without slipping. Since there is no slipping, the magnitude of the friction force is less than or equal to $\mu_s N$. Writing down Newton’s laws in the x- and y-directions, we have $\sum F_x= ma_x$ ; $\sum = F_y=ma_y$.
Substituting in from the free-body diagram:

$$mgsin \alpha −f_s =m(a_C)x$$
$$N - mg cos \alpha = 0$$,

we can then solve for the linear acceleration of the center of mass from these equations:

$$a_C =gsin \alpha - \frac{f_s}{m}$$However, it is useful to express the linear acceleration in terms of the moment of inertia. For this, we write down Newton’s second law for rotation,
$$\sum \tau_C=I_C \alpha$$

The torques are calculated about the axis through the center of mass of the cylinder. The only nonzero torque is provided by the friction force. We have

$$f_s r=I_C \alpha$$

Finally, the linear acceleration is related to the angular acceleration by

$$(a_C)x=r \alpha$$

These equations can be used to solve for $a_C$, $\alpha$, and $f_s$ in terms of the moment of inertia, where we have dropped the $x$-subscript. We write $a_C$ in terms of the vertical component of gravity and the friction force, and make the following substitutions.

$$f_s = \frac{I_C \alpha}{r} =\frac {I_C a_C}{r^2}$$.

From this we obtain

$$a_C=gsin \alpha− \frac{I_C a_C}{mr^2} =\frac {mgsin \alpha}{m+\frac{I_C}{r^2}}.$$

Because slipping does not occur, $f_s \le \mu_s N$. Solving for the friction force, $$f_s= \frac{mg I_C sin\alpha}{mr^2+I_C}.$$ Substituting this expression into the condition for no slipping, and noting that $$N = mg cos \alpha,$$ we have $$\frac{mg I_C sin\alpha}{mr^2+I_C} \le \mu_s mg cos\alpha,$$ or $$\mu_ s \ge \frac{tan \alpha}{1+\frac{mr^2}{I_C}}.$$ For a solid sphere: $$I_C = \frac{2}{5}m r^2.$$ So: $$\mu_s \ge \frac{2}{7} tan \alpha.$$ I think this result is not correct. Another friend of mine calculated it as $$ \mu_s \ge \frac{2 \sqrt{2} sin \alpha}{5 \sqrt{2} + 4},$$ but I don't know his method and probably it is not correct either. Could you please help me out?

 

[erobz]

The acompanying figure?

 

[Hak]

The acompanying figure?

I put it in, editing the "Homework statement".

 

[erobz]

About points 1. and 2., I assumed that the point of the sphere moving with maximum velocity is $Q$ and that the velocity at that point is $v_Q= 2v$. In fact, at the highest point of a rotating sphere, the velocity is given by the sum of the velocities of translation and rotation. Since, in a pure rolling condition, the two velocities are equal, then the velocity at $Q$ will be:
$$v_Q = v + v = 2v$$

I think $Q$ has the maximal velocity, but $Q$ having magnitude $2v$ doesn't feel right to me. It's $2v$ when it is rolling on a plane with a single point of contact that is instantaneously at rest, but here we have two points of contact, and they aren't at a distance $R$ from the center of mass?

I think I'm going to watch this one from the sidelines though.

 

[hmmm27]

If you can, please post the image directly (using the "Insert Image function in the edit-box), not as a link (which may break over time). thanks.1. You haven't actually said what you think the answer is.

[edit: okay, now we have an image, $Q$, right : also, it seems reasonable to assume that "from below" actually means "directly in front"]

2. Your assumption that $V_Q = 2v_{trans}$ is based on an incorrect assumption of how the ball is rolling . . . along the V-shaped track.

(As an aside, I'm assuming the question means by "falling" to be moving along the track, and not vertical displacement)

3. Kneejerk reaction says that the contact area is $0$ so there's no way of telling, so I guess my math/physics isn't immediately up to the task.

 

[Hak]

So what do you recommend we start with?

 

[hmmm27]

Who, me ? Well, your answer for #1 looks correct, so I'd start by taking a closer look at arriving at an answer for #2. #3 I'm going to bow out.

 

[kuruman]

I would use the parallel axes theorem to find the moment of inertia about the line joining the two points of contact which is the axis of rotation. If the axis of rotation is (instantaneously) stationary while the rest of the sphere rotates about it with some $\omega$ it should be obvious which point has the highest linear speed and what that speed is.

 

[Hak]

So, should I set the equation $$I_{AB} = I_c + Md^2$$? And I should solve for what? I didn't understand in a total way.

 

[erobz]

So, should I set the equation $$I_{AB} = I_c + Md^2$$? And I should solve for what? I didn't understand in a total way.

The location of the axis of rotation is relevant for question 2, and the M.o.I of the sphere about that axis is relevant for question 3 (I believe).

 

[Hak]

Assume the variable x for position of the point O and the angle \theta the part makes with the horizontal direction, and let be h the distance between O and C. Consider sequentially the velocities of points $O$, $C$ and $B$ when $x$ and $theta$ vary only.
$$v_O = \begin{pmatrix} \dot x \\ 0 \end{pmatrix}$$
$$v_B = \begin{pmatrix}\dot x + r \dot \theta \\ 0 \end{pmatrix}$$
$$v_C = \begin{pmatrix} \dot x + h \dot \theta cos \theta \\ h \dot \theta sin \theta \end{pmatrix},$$

where $\dot x$ and $\dot \theta$ are the first time derivatives.

Take the time derivative of the velocity at $C$ to get the acceleration of the center of mass.

$$a_C = \begin{pmatrix}\ddot x + h \ddot \theta cos \theta - h \ddot \theta^2 sin \theta \\ h \ddot \theta sin \theta - h \ddot \theta^2 cos \theta \end{pmatrix}$$

The equations of motion have to consider the balance of moments about the center of mass (point $C$) to be valid.

$$\begin{pmatrix} F_{friction} \\ N - mg \end{pmatrix} = ma_C$$ $\space$
$$- (h sin \theta) N + (r- h cos \theta) F_{friction} = I_C \ddot \theta$$

There are three equations and 4 unknowns. To solve them we need an expression descripting the contact condition.

No slipping - Solve with $$\dot x + r \dot \theta = 0$$, or $$\ddot x = - r \ddot \theta$$ for:

$$\ddot \theta = - \frac{hm(g + r \dot \theta^2) sin \theta}{I_C + m(r^2 + h^2 - 2hrcos \theta)}$$

$$\ddot x = \frac{rhm(g+r \dot \theta^2) sin \theta}{I_C + m(r^2 + h^2 -2hrcos \theta)}.$$

The center of rotation height above the ground is $$C = r+ \frac{\ddot x}{\ddot \theta} = 0,$$ so the body is always rotating about point B. This can be confirmed by the fact that the parallel axis theorem in the denominator of $\ddot \theta$ contains the distance between $B$ and $C$.

Friction - We have to solve with $$F_{friction} \le \mu N$$ for $\ddot x$, $\ddot \theta$ and $N$.

The math is complex, and I haven't been able to do it yet ( hints are appreciated). From this point on, I don't know how to proceed.

 

[erobz]

Shouldn’t you be able to ∑ torques about the axis of rotation to eliminate the effects of the contact /frictional forces?

 

[Hak]

Shouldn’t you be able to ∑ torques about the axis of rotation to eliminate the effects of the contact /frictional forces?

Can you give me a little hint?

P. S. Are my calculations correct?

 

[erobz]

Can you give me a little hint?

P. S. Are my calculations correct?

The axis of rotation of the sphere is the line connecting points A and B as @kuruman suggests. That is where you should take torques about as the normal and frictional forces have no moment arms with respect to that axis. Only the component of weight does. I think the first two questions beg of you to find that axis as a intermediate result to use in 3.

IMO, I don't believe your calculations are correct, but I haven't tried to work it myself yet.

 

[kuruman]

Part 2:
I don't understand "If $v$ is the speed at which the sphere falls $~\dots$" Which point on the sphere has this speed? Is it the CM?
For part 3:
You have two equations, Newton's second law for rotations and for linear motion along the incline. You also have two unknowns, the acceleration of the CM, $a_{cm}$, and the force of static friction, $f_s$. If you write the rotational dynamics equation with torque and moment of inertia calculated about the axis I suggested, you will get $a_{cm}$ as a fraction of $g\sin\!\alpha$ which is the sliding acceleration.

Knowing $a_{cm}$, the linear dynamics equation will give you the magnitude and direction of $f_s.$ A third Newton's second law in the vertical direction should give you the normal force $N$. Hint: It is not $mg\cos\!\alpha.$

Finally, the standard relation between maximum force of static friction and the normal force should give you the minimum value of $\mu_s$ given the incline angle $\alpha.$

 

[Hak]

Part 2:
I don't understand "If $v$ is the speed at which the sphere falls $~\dots$" Which point on the sphere has this speed? Is it the CM?

I think $v$ is the speed of the CM.

 

[Hak]

I cannot prove that $Q$ is the point with maximum velocity. However, I found the value of $v_Q$ by considering the following:

If the velocity at $AB$ is zero (we have no slipping about the axis of rotation), it sets the kinematic relation of $$v - \omega h = 0$$, where $h$ is the distance between $CM$ and the axis of rotation. The height difference between $AB$ and the center is $$h = r sin(\frac{\theta}{2})$$, where $r$ is the radius of the ball and $\theta = \frac{\pi}{2}$ is the angle between the two pieces of metal forming the V-shaped track. So: $$h = \frac{\sqrt{2}}{2} r$$. We have:
$$\omega = \frac{v}{h} = \sqrt{2} \frac{v}{r}$$. We have that $$v_{rot} = \omega r = \sqrt{2} v.$$
The velocity $v_Q$ is the sum of the velocity $v$ of CM and the rotational velocity $v_{rot}$, so:

$$v_Q = v + v_{rot} = v + \sqrt{2} v \Rightarrow v_Q = v(1+\sqrt{2})$$Now, consider the sums of forces and torques along the axes.

Sum of forces along track: $$mg sin \alpha - 2 F_{friction} = ma_{C}$$
Sum of forces perpendicular to track: $$2N - mg cos \alpha = 0$$
Sum of torques about the center of mass: $$2 F_{friction}h = I_C \frac{a_{C}}{h}$$, or, alternatively, about the axis of rotation: $$mghsin \alpha = (I_C + mh^2) \frac{a_{C}}{h}$$, where $\frac{a_{C}}{h}$ is the angular acceleration, obtained by deriving $\omega$.

Solving the above three equations for $a_C$, $F_{friction}$ and $N$, we have

$$a_{C} = \frac{mgh^2 sin \alpha}{I_C + mh^2}$$
$$F_{friction} = \frac{I_C mg sin \alpha}{2(I_C + mh^2)}$$
$$N = \frac{mg cos \alpha}{2}$$
Note the denominator is the mass moment of inertia about $AB$, same as what you found using the parallel axis theorem.
Using $$F_{friction} \le \mu N$$, we have that: $$\mu \ge \frac{F_{friction}}{N} \Rightarrow \mu_{min} = \frac{F_{friction}}{N} = \frac{2 I_C mg sin \alpha}{2(I_C + mh^2)mg cos \alpha}$$. Substituting in $h = \frac{\sqrt{2}}{2} r$ and $I_C = \frac{2}{5} mr^2$, we have:
$$\mu_{min} = \frac{4}{9} tan \alpha.$$

Let me know what do you think about it. I apologize for the briefness; I usually write the steps much more in-depth, but I am quite tired.

 

[erobz]

I cannot prove that $Q$ is the point with maximum velocity. However, I found the value of $v_Q$ by considering the following:

If the velocity at $AB$ is zero (we have no slipping about the axis of rotation), it sets the kinematic relation of $$v - \omega h = 0$$, where $h$ is the distance between $CM$ and the axis of rotation. The height difference between $AB$ and the center is $$h = r sin(\frac{\theta}{2})$$, where $r$ is the radius of the ball and $\theta = \frac{\pi}{2}$ is the angle between the two pieces of metal forming the V-shaped track. So: $$h = \frac{\sqrt{2}}{2} r$$. We have:
$$\omega = \frac{v}{h} = \sqrt{2} \frac{v}{r}$$. We have that $$v_{rot} = \omega r = \sqrt{2} v.$$
The velocity $v_Q$ is the sum of the velocity $v$ of CM and the rotational velocity $v_{rot}$, so:

$$v_Q = v + v_{rot} = v + \sqrt{2} v \Rightarrow v_Q = v(1+\sqrt{2})$$

Thats what I'm getting.

Sum of forces perpendicular to track: $$2N - mg cos \alpha = 0$$

I don't think that is correct. Draw Normals is the front view, resolve them into components then further resolve those components into components in the sideview.

 

[Hak]

I don't think I understood correctly. Could I have some hints?

 

[erobz]

I don't think I understood correctly. Could I have some hints?

Think about the direction of the Normals in 3 dimensional space. When you are looking from the side view are you seeing the true length of the vector or the projection of the vector onto the viewing plane?

 

[Hak]

Obviously, the projection of the vector onto the viewing plane, but I cannot express it in physical formulas. Should I also consider the horizontal component of $N$?

 

[erobz]

Obviously, the projection of the vector onto the viewing plane, but I cannot express it in physical formulas. Should I also consider the horizontal component of $N$?

Draw Normals in the front view. It is the vertical component of the Normals in the front view that is balancing the forces in the side view, not the entire magnitude of the normal vectors.

 

[Hak]

So, is $2N cos \alpha = mg$ correct?

 

[erobz]

So, is $2N cos \alpha = mg$ correct?

No, look at the front view, i.e. the view on the right of the image you attached. Draw the Normals in that view.

 

[Hak]

I have $N_A = mg cos \alpha$ and $N_B = mg sin \alpha$. So?

 

[erobz]

The vertical components of the normal forces in this picture. They are what balance the component of weight perpendicular to the incline in the side view.

 

[Hak]

Why did you only consider the normal force in $B$? Sorry to bother repeatedly...

 

[erobz]

Why did you only consider the normal force in $B$? Sorry to bother repeatedly...

I didn't. That was just an illustration of what I'm talking about. Do you understand what I'm saying about this whole normal force business yet?

 

[Hak]

I don't know if I understood. I would say $N (cos \alpha + sin \alpha) = mg cos \alpha$. Is it correct?

 

[erobz]

I don't know if I understood. I would say $N (cos \alpha + sen \alpha) = mg cos \alpha$. Is it correct?

Sorry, you aren’t seeing it yet.

 

[Hak]

I don't know how to do it. You said that the vertical components of the normal forces must balance the perpendicular weight $mg cos \alpha$. So, what is wrong in my equation should be the expression of $N$, right? Would you have more in-depth hints on how to write it?

 

[erobz]

I don't know how to do it. You said that the vertical components of the normal reaction must balance the perpendicular weight $mg cos \alpha$. So, what is wrong in my equation should be the expression of $N$, right? Would you have more in-depth hints on how to write it?

The component of weight is in the plane of the page. The normal force is pointing into the page at a 45 degree angle. It is only the component of $N$ parallel to the plane of the page which balances the component of weight...not the entire magnitude $N$.

 

[Hak]

Yes, you're right. $N \sqrt{2} = mg cos \alpha$ is correct actually?

 

[Hak]

So, is the correct solution $\mu_{min} = \frac {2 \sqrt{2}}{9} tan \alpha?$

 

[kuruman]

I cannot prove that ##Q is the point with maximum velocity.

Look at the figure below. The axis of rotation is the red dotted line AB. All points on the sphere rotate about that axis with a common angular velocity $\mathbf{\omega}$. Their linear velocity relative to AB, which is at rest relative to the track, is $\mathbf{v}=\mathbf{\omega}\times \mathbf{r}.$ Here, $\mathbf{r}$ is the position vector of a point on the sphere perpendicular to the axis AB. How do you find the point at which $\mathbf{v}$ has the largest magnitude?