- #1
Nexus99
- 103
- 9
- Homework Statement
- Work in progress
- Relevant Equations
- Pure rolling condition
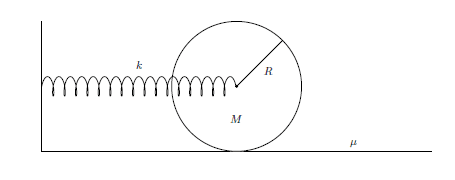
A homogeneous sphere of mass M and radius R is at rest on a rough horizontal plane with coefficient
of static friction μ . A spring of elastic constant k, is connected to the rotation axis of the sphere
illustrated in the figure. The center of mass of the sphere is positioned at rest so that the spring is
lengthened by a stretch equal to L, determine:
a) the period of oscillations of the sphere;
b) the maximum angular velocity of the sphere;
c) the maximum value of L for which the pure rolling speed is maintained.
 I tried in this way:
I tried in this way:
a) if there is an oscillation there is no static friction but dynamic:
Projecting the two cardinal equations along the axis and considering the center of mass of the sphere the point about which the torque is being measured:
-F_{r} - kL = ma
F_{r}R = Ialpha = I a/R = 2/5MRa
F_{r} = 2/5Ma
- 5/7kL = ma k' = 5/7k
-k'L = ma
that is the equation of an harmonic oscillator with ω = √(5/7 k m), that represent the period of oscillations of the sphere, is this solution right?
of static friction μ . A spring of elastic constant k, is connected to the rotation axis of the sphere
illustrated in the figure. The center of mass of the sphere is positioned at rest so that the spring is
lengthened by a stretch equal to L, determine:
a) the period of oscillations of the sphere;
b) the maximum angular velocity of the sphere;
c) the maximum value of L for which the pure rolling speed is maintained.
a) if there is an oscillation there is no static friction but dynamic:
Projecting the two cardinal equations along the axis and considering the center of mass of the sphere the point about which the torque is being measured:
-F_{r} - kL = ma
F_{r}R = Ialpha = I a/R = 2/5MRa
F_{r} = 2/5Ma
- 5/7kL = ma k' = 5/7k
-k'L = ma
that is the equation of an harmonic oscillator with ω = √(5/7 k m), that represent the period of oscillations of the sphere, is this solution right?
Last edited by a moderator: