huc369
- 7
- 0
- TL;DR
- How is the intermediate displacement speed derived?
I don't know if I wrote it correctly
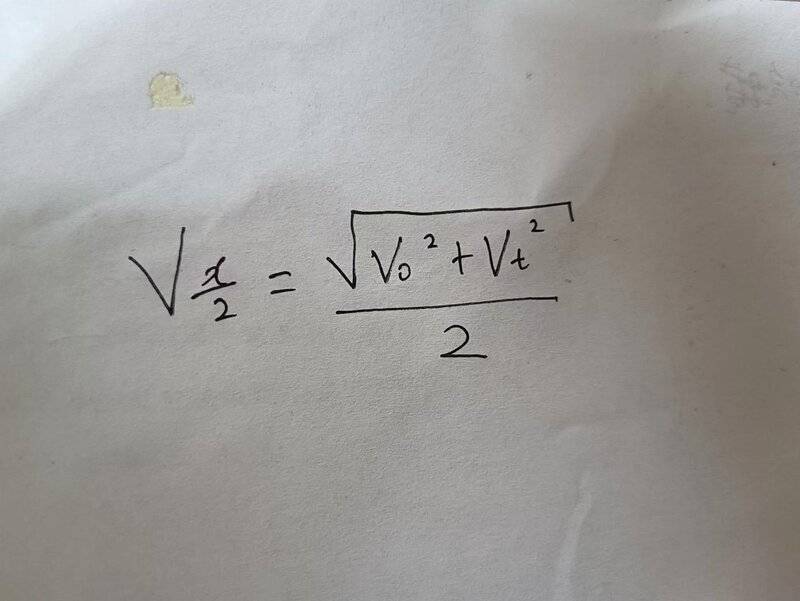
The discussion focuses on the derivation of intermediate displacement speed using the SUVAT equations, which apply to scenarios involving constant acceleration. The correct formula for intermediate displacement speed is established as v_B = \sqrt{ \frac{(v_0)^2 + (v_T)^2}{2} }, correcting the initial misinterpretation. The conversation emphasizes the importance of formulating clear questions in scientific discussions to facilitate understanding and problem-solving.
Students of physics, educators teaching kinematics, and anyone interested in understanding motion dynamics and the application of SUVAT equations.
Thank you very much, I will google itPeroK said:SUVAT
Since SUVAT involves constant-acceleration,huc369 said:Summary: How is the intermediate displacement speed derived?
I don't know if I wrote it correctlyView attachment 315157