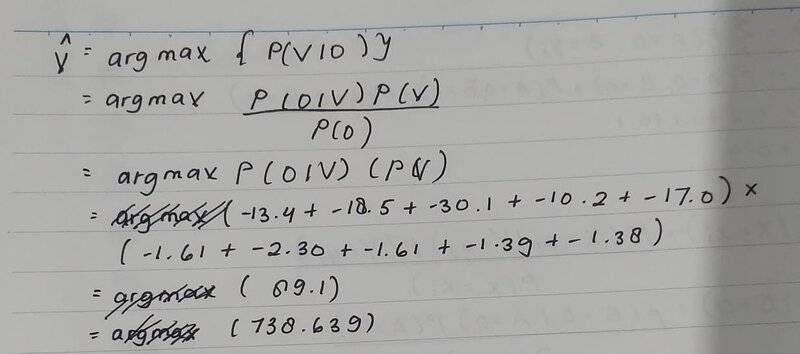Discussion Overview
The discussion revolves around the application of acoustic and language models in a probabilistic framework, specifically focusing on maximizing the conditional probability of a vowel given a feature vector. Participants are exploring the implications of the equations and terms involved, such as "argmax" and the role of log likelihoods in the context of a homework problem.
Discussion Character
- Homework-related
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant presents a homework problem involving the maximization of the conditional probability P(V|O) using acoustic and language models.
- Another participant questions the meaning of "argmax" and its relation to the logarithmic form of probabilities, suggesting a lack of clarity in the original post.
- Concerns are raised about the calculations presented, particularly regarding the addition of numbers from the log table and the method of maximizing the product of probabilities.
- A participant expresses uncertainty about the correctness of the initial approach and suggests that the original poster may benefit from consulting their instructor for further guidance.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correctness of the original work. There are differing interpretations of the calculations and the definitions of terms like "argmax," indicating unresolved disagreements.
Contextual Notes
Limitations include a lack of definitions for key terms such as "argmax," and uncertainty about the role of the log table numbers in the calculations. The discussion does not clarify the assumptions underlying the problem or the specific context of the models being used.
Who May Find This Useful
Students and educators interested in probabilistic models in linguistics or acoustic processing may find this discussion relevant, particularly those working on similar homework problems or exploring the concepts of conditional probabilities and model maximization.