HumanistEngineer
- 18
- 2
Hello All,
I want to improve myself in data fitting in order to derive new equations for the data from experimental results and/or performance analysis. I am an engineering researcher and since I found some out-of-world formulations derived from performance data, I need to learn this advanced data fitting (or whatever its name is) discipline.
Please guide me to the exact field name and/or books to achieve this skill. I guess that this is not just Math but also Physics so that one could put the relationship between the input data and/or dimensionless quantities.
For example: How come one could derive this formulation for the correction factor data (LMTD heat exchanger) as shown below:
Here is the formulation/expression:
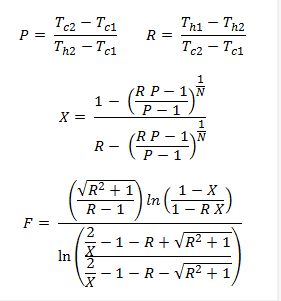
For the graph:
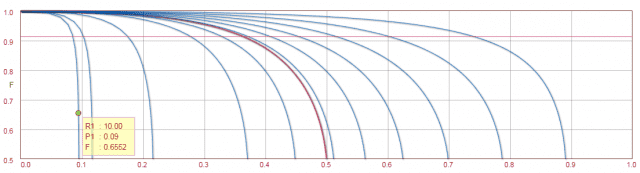
Thank you in advance.
I want to improve myself in data fitting in order to derive new equations for the data from experimental results and/or performance analysis. I am an engineering researcher and since I found some out-of-world formulations derived from performance data, I need to learn this advanced data fitting (or whatever its name is) discipline.
Please guide me to the exact field name and/or books to achieve this skill. I guess that this is not just Math but also Physics so that one could put the relationship between the input data and/or dimensionless quantities.
For example: How come one could derive this formulation for the correction factor data (LMTD heat exchanger) as shown below:
Here is the formulation/expression:
For the graph:
Thank you in advance.