Plotting a Scatter Diagram from a Large Data Set

[AN630078]

Homework Statement

Hello, I have bee revising my understanding of statistics specifically bivariate data and the AQA A Level Mathematics Large Data Set. I have found the question below which I am hopelessly struggling with.
I have attached a copy of the data set here.

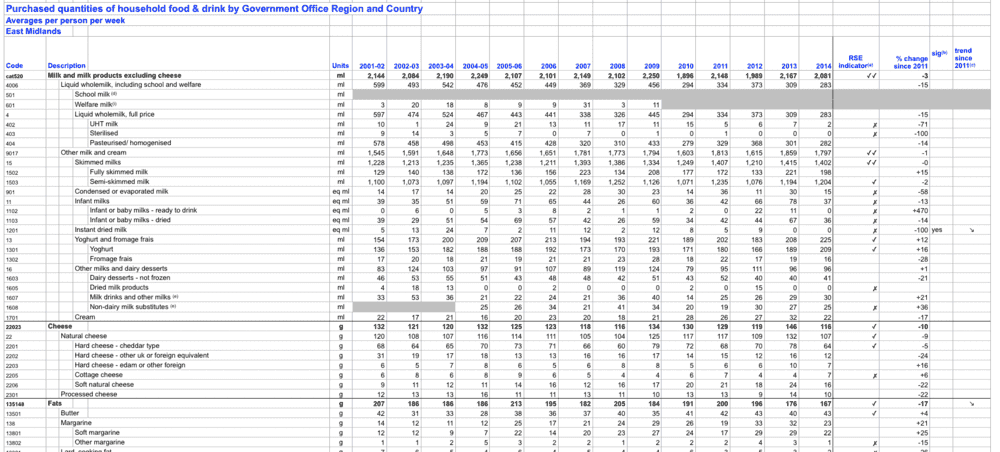
Using the data for the purchased quantities of food in the East Midlands from the LDS, plot a scatter diagram to investigate any correlation between purchased quantities of butter and margarine using data from 2006-2014.
Plot margarine on the x-axis. Give your conclusions, including comments on the suitability of data.

Relevant Equations

r

So I have attempted to plot the scatter diagram. My first query is does the question intend for you to include both subsets of data on one axis, (which I have plotted on the x-axis) or rather does it demand two separate diagrams to investigate if there is any correlation, or a single diagram? I understand that in a scatter diagram the independent variable is plotted on the x-axis and the dependent variable on the y-axis. Since I did not think that either purchased quantities of butter nor margarine are dependent on each other I took them both to be independent variables and plot them on the x-axis.
Moreover, I have attempted to draw regression lines for each data set (lines of best fit) to better evaluate the distribution of the data, but do not think that I have done so accurately enough.

In the first diagram I have attached I believe that of the purchased quantities of butter the variables increase together thereby exhibiting a positive correlation, and presumably the correlation coefficient r has a positive value where r >0.
Similarly, of the purchased quantities of margarine the variables predominantly increase together and exhibit a positive correlation, however, this correlation is not as strong as for margarine and does include more outlying data points.
Moreover, the purchased quantities of butter continue to exceed that of margarine between 2006-2014 although there is a notable decline in the purchase of butter in 2009.
In terms of the suitability of the data, I believe that it is an extensive sample as it is divided among the regions of the UK and further collected to calculate an average for the purchased quantities per week, which is a very regular basis as opposed to say a month or year. The data extends from 2006-2014 which is a moderate time period to evaluate any changes in trend, although this could be extended from an earlier date to evaluate previous purchased quantities to broaden the data set and search for any further outliers. In this sense, the data is limited as it only concerns purchased quantities from 2006-2014 and excludes any previous or contemporary data.

However, would I instead plot the purchased quantities of margarine on the x-axis and thus the remaining variable, the purchased quantities of butter on the y-axis since a scatter diagram intends to show each pair of data values as a single point on the graph and to exhibit the type and strength of relationship between the two variables.
I have also done so and attached the graph here. In which case, I believe that the two variables are shown to be exhibit moderate positive correlation, especially discernible for the latter three points on the diagram. However, would it be more suitable to state that as a whole the bivariate data is uncorrelated and has zero correlation, i.e. a value of 0 for the correlation coefficient r=0?

I really want to improve upon my plotting of scatter diagrams and interpretation of data. How could I correct or improve upon my answer here, clearly I am rather confused but I am trying to comprehensively evaluate the information given. I would be very grateful of any response, sorry to ask here I just do not have anyone else who can help me.

[Moderator's note: The data set had a copyright note, so I removed it.]

 

[pbuk]

You should read the question more carefully.

So I have attempted to plot the scatter diagram. My first query is does the question intend for you to include both subsets of data on one axis,

No, it tells you to "Plot butter on the x-axis." (not plot butter and margarine on the x-axis).

or rather does it demand two separate diagrams to investigate if there is any correlation?

No it tells you to "plot a scatter diagram" (not "plot two diagrams").

Since I did not think that either purchased quantities of butter nor margarine are dependent on each other I took them both to be independent variables and plot them on the x-axis.

The question asks you to "investigate any correlation between purchased quantities of butter and margarine", it does not ask you to guess whether there is a correlation or not and then do something else.

Moreover, I have attempted to draw regression lines for each data set (lines of best fit) to better evaluate the distribution of the data, but do not think that I have done so accurately enough.

You have plotted consumption on the x-axis and time (in years) on the y-axis. Have you ever seen time plotted on the y-axis before?

However, would I instead plot the purchased quantities of margarine on the x-axis and thus the remaining variable, the purchased quantities of butter on the y-axis since a scatter diagram intends to show each pair of data values as a single point on the graph and to exhibit the type and strength of relationship between the two variables.

Well this would make more sense, but it tells you to "Plot butter on the x-axis", so what do you think you should plot on the y-axis?

 

[AN630078]

You should read the question more carefully.No, it tells you to "Plot butter on the x-axis." (not plot butter and margarine on the x-axis).No it tells you to "plot a scatter diagram" (not "plot two diagrams").The question asks you to "investigate any correlation between purchased quantities of butter and margarine", it does not ask you to guess whether there is a correlation or not and then do something else.You have plotted consumption on the x-axis and time (in years) on the y-axis. Have you ever seen time plotted on the y-axis before?Well this would make more sense, but it tells you to "Plot butter on the x-axis", so what do you think you should plot on the y-axis?

Thank you for your reply. Sorry, a typo in the original question it is maragarine on the x-axis. Yes, since it states a scatter diagram that is why I leant towards a single graph.
Yes, actually I saw a graph plotting two groups of data showing the populations in different areas by the time in years on the y-axis, which I confessedly used as a partial basis for my first diagram.

I think I should plot butter in the y-axis then, as in the second diagram.

 

[pbuk]

Thank you for your reply. Sorry, a typo in the original question it is maragarine on the x-axis. Yes, since it states a scatter diagram that is why I leant towards a single graph.
...
I think I should plot butter in the y-axis then, as in the second diagram.

Yes, that looks right - although starting the axes at 0 means most of the page is empty. You might lose a mark for this.

In which case, I believe that the two variables are shown to be exhibit moderate positive correlation, especially discernible for the latter three points on the diagram.

I can't see any correlation from that plot, and looking at the last 3 plots in isolation tells you nothing. You would get 0 marks for this. I find it surprising that the question has been set this way - it is often taught in elementary economics that consumption of products like butter and margarine are negatively correlated because they are substitutes, but that is not what the data show here.

However, would it be more suitable to state that as a whole the bivariate data is uncorrelated and has zero correlation, i.e. a value of 0 for the correlation coefficient r=0?

No, the question only asks you to "plot a scatter diagram to investigate any correlation" so I can't see any marks for investigating the correlation any other way. For this dataset I calculated r as 0.26, not 0.

Yes, actually I saw a graph plotting two groups of data showing the populations in different areas by the time in years on the y-axis, which I confessedly used as a partial basis for my first diagram.

Wow. The person that plotted this chart must have been trying to demonstrate that time depends on the population of a number of geographical areas. Interesting.

 

[AN630078]

Yes, that looks right - although starting the axes at 0 means most of the page is empty. You might lose a mark for this.I can't see any correlation from that plot, and looking at the last 3 plots in isolation tells you nothing. You would get 0 marks for this. I find it surprising that the question has been set this way - it is often taught in elementary economics that consumption of products like butter and margarine are negatively correlated because they are substitutes, but that is not what the data show here.No, the question only asks you to "plot a scatter diagram to investigate any correlation" so I can't see any marks for investigating the correlation any other way. For this dataset I calculated r as 0.26, not 0.Wow. The person that plotted this chart must have been trying to demonstrate that time depends on the population of a number of geographical areas. Interesting.

Thank you very much for your reply.

I agree, I have redrawn my scatter diagram and attached it for your perusal. I have included a zigzag on both of the axis to reduce the empty space, I think this has benefited overall evaluation of the graph. I have also attempted to draw a line of best fit.
To better answer the question concerning the correlation of butter and margarine I would state that there is zero correlation, or only a very minor positive correlation as you have shown that r does not equal 0 but 0.26. A weak positive correlation demonstrates that people who buy more margarine tend to purchase more butter, but not always, and vice versa. That is rather logical as they are similar products, and to a certain extent, can be used for the same purpose, or as you stated are substitutes.

I am sorry I have not been taught how to calculate the coefficient of correlation, I just know from a textbook that the value of r is -1<r<1 and is:

• r=1 for perfect positive correlation
• r=0 for negative correlation
• r=-1 for perfect negative correlation

Since the data did not appear to exhibit any correlation I took this to mean that it was exhibiting zero correlation, hence r=0, but clearly I was too hasty in my assumptions.

Haha, yes in hindsight I think it must have been a rather peculiar graph of the two population data sets set against time

Moreover, in commenting on the suitability of the data do you think that I could improve upon my previous thoughts:

"In terms of the suitability of the data, I believe that it is an extensive sample as it is divided among the regions of the UK and further collected to calculate an average for the purchased quantities per week, which is a very regular basis as opposed to say a month or year. The data extends from 2006-2014 which is a moderate time period to evaluate any changes in trend, although this could be extended from an earlier date to evaluate previous purchased quantities to broaden the data set and search for any further outliers. In this sense, the data is limited as it only concerns purchased quantities from 2006-2014 and excludes any previous or contemporary data."

Thank you very much again for your help