Aju051000's questions at Yahoo Answers involving trigonometry

[MarkFL]

Here are the questions:

Trigonometry help please!?

Ok so our teacher gave us 34 questions to do for an assignment and I got all of them except two :( Please help me figure these out!

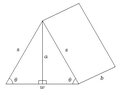
A two-person tent is to be made so that the height at the center is a = 4 feet (see the figure below). If the sides of the tent are to meet the ground at an angle 60°, and the tent is to be b = 8 feet in length, how many square feet of material will be needed to make the tent? (Assume that the tent has a floor and is closed at both ends, and give your answer in exact form.)

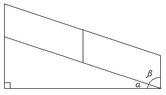
The figure below shows a walkway with a handrail. Angle α is the angle between the walkway and the horizontal, while angle β is the angle between the vertical posts of the handrail and the walkway. Use the figure below to work the problem. (Assume that the vertical posts are perpendicular to the horizontal.)
Find α if β = 62°.

thank you so so much!

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello aju051000,

1.) I would first draw a diagram:

View attachment 1246

We are given the following:

\(\displaystyle a=4\text{ ft},\,b=8\text{ ft},\,\theta=60^{\circ}\)

So, we need to find the $s$ and $w$. We may use:

\(\displaystyle \tan\left(60^{\circ} \right)=\frac{a}{w/2}=\frac{2a}{w}\)

\(\displaystyle w=2a\cot\left(60^{\circ} \right)=\frac{8}{\sqrt{3}}\text{ ft}\)

We should recognize that the triangular ends of the tent are equilateral (and so $s=w$), but if we didn't we could write:

\(\displaystyle \sin\left(60^{\circ} \right)=\frac{a}{s}\)

\(\displaystyle s=a\csc\left(60^{\circ} \right)=\frac{8}{\sqrt{3}}\text{ ft}\)

So, to find the surface area of the tent, we see that there are two congruent triangles and 3 congruent rectangles.

The area of the two triangles is:

\(\displaystyle A_T=2\cdot\frac{1}{2}\cdot\frac{8}{\sqrt{3}}\text{ ft}\cdot4\text{ ft}=\frac{32}{\sqrt{3}}\text{ ft}^2\)

The area of the three rectangles is:

\(\displaystyle A_R=3\cdot\frac{8}{\sqrt{3}}\text{ ft}\cdot8\text{ ft}=64\sqrt{3}\text{ ft}^2\)

Hence, the total surface area $A$ of the tent is:

\(\displaystyle A=A_T+A_R=\frac{32}{\sqrt{3}}\text{ ft}^2+64\sqrt{3}\text{ ft}^2=\frac{224}{\sqrt{3}}\text{ ft}^2\)

2.) Again, let's first draw a diagram:

View attachment 1247

We can now easily see that $\alpha$ and $\beta$ are complementary, hence:

\(\displaystyle \alpha+\beta=90^{\circ}\)

\(\displaystyle \alpha=90^{\circ}-\beta\)

With $\beta=62^{\circ}$, we find:

\(\displaystyle \alpha=(90-62)^{\circ}=28^{\circ}\)