Alexander's question via email about Newton's Method

[Prove It]

Alexander asks:

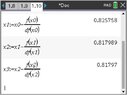
Apply three iterations of Newton's Method to find an approximate solution of the equation

$\displaystyle \mathrm{e}^{1.2\,x} = 1.5 + 2.5\cos^2{\left( x \right) } $

if your initial estimate is $\displaystyle x_0 = 1 $.

What solution do you get?

 

[jedishrfu]

@Prove It answers:

Newton's Method solves an equation of the form $\displaystyle f\left( x \right) = 0 $, so we need to rewrite the equation as

$\displaystyle \mathrm{e}^{1.2\,x} - 1.5 - 2.5\cos^2{\left( x \right) } = 0 $

Thus $\displaystyle f\left( x \right) = \mathrm{e}^{1.2\,x} - 1.5 - 2.5\cos^2{\left( x \right) }$.

Newton's Method is: $\displaystyle x_{n+1} = x_n - \frac{f\left( x_n \right) }{f'\left( x_n \right) } $

We will need the derivative, $\displaystyle f'\left( x \right) = 1.2\,\mathrm{e}^{1.2\,x} + 5\sin{\left( x \right) }\cos{\left( x \right) } $.I have used my CAS to do this problem:

View attachment 9644

View attachment 9645

So after three iterations the root is approximately $\displaystyle x_3 = 0.81797 $.