All Possible Sortings of a DAG - Hello! (Wave)

  • MHB
  • Thread starter evinda
  • Start date
In summary, the conversation discusses finding all possible topological sortings in a DAG. The first person shares a program they found but doesn't fully understand, and the second person suggests using an adjacency matrix to find the sortings. They then discuss their own algorithm, which involves repeatedly selecting the first node with all incoming dependencies satisfied and adding it to an output list. The conversation continues with clarifications and improvements to the algorithm, ultimately resulting in a revised version that uses a set of starting nodes and an output set to process the nodes.
  • #1
evinda
Gold Member
MHB
3,836
0
Hello! (Wave)

Suppose that we have a DAG and want to find algorithmically all its possible topological sortings.
I found this program at page 6: http://www.cs.ncl.ac.uk/publications/trs/papers/61.pdf, but I haven't really understood it.
Could you explain me the general idea?
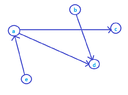
How would it work for example if we had the following graph?View attachment 4228
 

Attachments

  • top.png
    top.png
    3 KB · Views: 83
Technology news on Phys.org
  • #2
Also I thought that we could also find all the possible sortings with an adjacency matrix.

I have thought of the following algorithm:Let $S$ be the set of the starting nodes.

Code: 
while (S!=empty set){
         pick a node q from S
         Alg(q)
}

Code: 
Alg(q){
     for i=1 to |V|{
          if A(q,i)==1{ // A is the adjacency matrix
             A(q,i)=0
             Enqueue(Q,q)
             Alg(i)
           }
     }
     Dequeue(Q)
 }
Is the general idea right? If so what could I improve at the algorithm? (Thinking)
 
  • #3
I don't know about that paper, but I have an idea how to do it. (Thinking)

Suppose we repeatedly run through the nodes and pick the first node that has all incoming dependencies satisfied.
We'll append that to an output list that is initially empty.

In the first run nodes b and e are the only nodes that have no arrows pointing to them.
So we pick b as the first node and get the output list (b).

In the second run e is the only node available, yielding (b, e).

In the third run a has become available, since its dependency on e is now satisfied.
So we get (b, e, a).

Next is c. And finally we get to d.
So our list has become (b, e, a, c, d). (Happy)
 
  • #4
I like Serena said:
Suppose we repeatedly run through the nodes and pick the first node that has all incoming dependencies satisfied.
We'll append that to an output list that is initially empty.

In the first run nodes b and e are the only nodes that have no arrows pointing to them.
So we pick b as the first node and get the output list (b).

In the second run e is the only node available, yielding (b, e).

In the third run a has become available, since its dependency on e is now satisfied.
So we get (b, e, a).

Next is c. And finally we get to d.
So our list has become (b, e, a, c, d). (Happy)

To do this, could we use the adjacency matrix as I did in post #2? (Thinking)
 
  • #5
evinda said:
Code: 
while (S!=empty set){
         pick a node q from S
         Alg(q)
}
Code: 
Alg(q){
     for i=1 to |V|{
          if A(q,i)==1{ // A is the adjacency matrix
             A(q,i)=0
             Enqueue(Q,q)
             Alg(i)
           }
     }
     Dequeue(Q)
 }

evinda said:
To do this, could we use the adjacency matrix as I did in post #2? (Thinking)

Let's see... (Thinking)

First node we might pick is q=a.
So we would execute Alg(a).
Searching the adjacency matrix, we find that a is connected to c.
So we remove that connection, we enqueue a, and continue with Alg(c).

But... node a is not suitable to select as first node. :eek:

I think I don't understand your algorithm.
Can you clarify? (Wondering)
 
  • #6
I like Serena said:
Let's see... (Thinking)

First node we might pick is q=a.
So we would execute Alg(a).
Searching the adjacency matrix, we find that a is connected to c.
So we remove that connection, we enqueue a, and continue with Alg(c).

But... node a is not suitable to select as first node. :eek:

I think I don't understand your algorithm.
Can you clarify? (Wondering)

$S$ is the set of starting nodes, that means it contains all the vertices with no incoming edges. So $a$ cannot be selected as first node. (Thinking)
 
  • #7
evinda said:
$S$ is the set of starting nodes, that means it contains all the vertices with no incoming edges. So $a$ cannot be selected as first node. (Thinking)

Can you run through your algorithm then and explain how the nodes get processed? (Wondering)
 
  • #8
I like Serena said:
Can you run through your algorithm then and explain how the nodes get processed? (Wondering)

I changed a little the algorithm.

Code: 
S: set of starting nodes 
L: output set 

while (S != empty) 
     pick a node q and delete it from S 
     Alg(q)k=0;
Alg(q){
     add q into L
     for i=1 to |V| {
          if (A(q,i)==1){
               A(q,i)=0
               for j=1 to |V| {
                    if (A(j,i)==1)
                        k=k+1;
               }
               if (k==|V|)
                    add i to S
               Alg(i)
          }
     }
}
At the beginning we have $S=\{b,e\}$. We pick $q=b$, delete it from $S$, so $S=\{e\}$.
We call [m]Alg(b)[/m] and we add $b$ into $L$, so $L=\{b\}$.
[m]A(b,d)==1[/m]
We set [m]A(b,d)=0[/m], $d$ has still incoming edges so we don't add it into $S$.
We call [m]Alg(d)[/m] and we add $d$ into $L$, so $L=\{b,d\}$.
The condition [m]A(d,i)[/m] is never satisfied so we go back at the while-loop.
We pick $q=e$, delete it from $S$, so $S=\{ \}$.
We call [m]Alg(e)[/m] and we add $e$ into $L$, so $L=\{b,d,e\}$.
[m]A(e,a)==1[/m]
We set [m]A(e,a)=0[/m], $a$ has no incoming edges so we add it into $S$, so $S=\{a\}$.
We call [m]Alg(a)[/m] and we add $a$ into $L$, so $L=\{b,d,e,a\}$.
[m]A(a,c)==1[/m]
We set [m]A(a,c)=0[/m], $c$ has no incoming edges so we add it into $S$, so $S=\{c\}$.
We call [m]Alg(c)[/m] and we add $c$ into $L$, so $L=\{b,d,e,a,c\}$.
The condition [m]A(c,i)[/m] is never satisfied so we go back at the while-loop and since $S$ is empty, we have finished.

Is it right? (Thinking)

But...can we find in that way all the possible topological sortings or only one? (Thinking)
 
  • #9
evinda said:
At the beginning we have $S=\{b,e\}$. We pick $q=b$, delete it from $S$, so $S=\{e\}$.
We call [m]Alg(b)[/m] and we add $b$ into $L$, so $L=\{b\}$.
[m]A(b,d)==1[/m]
We set [m]A(b,d)=0[/m], $d$ has still incoming edges so we don't add it into $S$.
We call [m]Alg(d)[/m] and we add $d$ into $L$, so $L=\{b,d\}$.

Wait! (Wait)

You just said that $d$ still had incoming edges.
Doesn't that mean that it is too early to add it to $L$? (Wondering)
 
  • #10
I like Serena said:
Wait! (Wait)

You just said that $d$ still had incoming edges.
Doesn't that mean that it is too early to add it to $L$? (Wondering)

I changed again something..

Code: 
S: set of starting nodes 
L: output set 

while (S != empty) 
     pick a node q and delete it from S 
     Alg(q)
Alg(q){
     for i=1 to |V| {
          if (A(q,i)==1){
               A(q,i)=0
               Alg(i)
          }
     }
     add q into L
}
Now we get this output: [m] L={d,b,c,a,e} [/m]Is this output right? (Thinking)
 
  • #11
Now I read that "The Floyd–Warshall algorithm compares all possible paths through the graph between each pair of vertices."

Could we take this into consideration in order to find all the possible topological sortings? (Thinking)
 
  • #12
evinda said:
Now we get this output: [m] L={d,b,c,a,e} [/m]

Is this output right? (Thinking)

Node d has incoming arrows, so I don't think it should be first in the list. (Worried)
evinda said:
Now I read that "The Floyd–Warshall algorithm compares all possible paths through the graph between each pair of vertices."

Could we take this into consideration in order to find all the possible topological sortings? (Thinking)

That seems to be an algorithm to find a shortest path.
How would that help to find a topological ordering? (Wondering)
 
  • #13
I like Serena said:
Node d has incoming arrows, so I don't think it should be first in the list. (Worried)

I changed again the algorithm:

Code: 
S: set of starting nodes 
    L: output set 
    
    while (S != empty) 
         pick a node q, delete it from S and add it into L
         Alg(q)
    
    
    
    Alg(q){
         for i=1 to |V| {
              if (A(q,i)==1){
                   A(q,i)=0
              }
              for j=1 to |V| { 
                   if (A(j,i)==0){ 
                       k=k+1
                   } 
              } 
              if (k==|V|){ 
                  add i into S 
              }
         }
    }
Now I get this output set: {b,e,a,c,d}.
Is it right? (Thinking)
 
  • #14
But can we get in that way all the possible topological sortings? (Thinking)
 
  • #15
evinda said:
I changed again the algorithm:

Code: 
S: set of starting nodes 
    L: output set 
    
    while (S != empty) 
         pick a node q, delete it from S and add it into L
         Alg(q)
    
    
    
    Alg(q){
         for i=1 to |V| {
              if (A(q,i)==1){
                   A(q,i)=0
              }
              for j=1 to |V| { 
                   if (A(j,i)==0){ 
                       k=k+1
                   } 
              } 
              if (k==|V|){ 
                  add i into S 
              }
         }
    }
Now I get this output set: {b,e,a,c,d}.
Is it right? (Thinking)

Yep. I think so. (Nod)
evinda said:
But can we get in that way all the possible topological sortings? (Thinking)

Not really... you'll only find one possible sorting... (Wasntme)

To get all possible sortings, you'll need a backtracking algorithm. (Thinking)

The standard format of backtracking is:
Code: 
Recurse()
	Create list of choices
	If no choices and solution found
		Output solution
	For each possible choice
		Execute choice
		Recurse()
		Undo choice

You can do that in your case for instance as follows:

Code: 
    S: set of starting nodes 
    L: output set 
    A: adjacency matrix

    Recurse()    
    
    Recurse(){
         if S empty
            output L
         oldA = A
         oldS = S
         oldL = L
         // For each possible choice
         for each node q in S
             // Execute choice
             delete q from S and add it to L
             Alg(q)
             // Recurse
             Recurse()
             // Undo choice
             S = oldS
             L = oldL
             A = oldA
    }
    
    Alg(q){
         for i=1 to |V| {
              if (A(q,i)==1){
                   A(q,i)=0
              }
              for j=1 to |V| { 
                   if (A(j,i)==0){ 
                       k=k+1
                   } 
              } 
              if (k==|V|){ 
                  add i into S 
              }
         }
    }
 
  • #16
I like Serena said:
Yep. I think so. (Nod)

Not really... you'll only find one possible sorting... (Wasntme)

To get all possible sortings, you'll need a backtracking algorithm. (Thinking)

The standard format of backtracking is:
Code: 
Recurse()
	Create list of choices
	If no choices and solution found
		Output solution
	For each possible choice
		Execute choice
		Recurse()
		Undo choice

You can do that in your case for instance as follows:

Code: 
    S: set of starting nodes 
    L: output set 
    A: adjacency matrix

    Recurse()    
    
    Recurse(){
         if S empty
            output L
         oldA = A
         oldS = S
         oldL = L
         // For each possible choice
         for each node q in S
             // Execute choice
             delete q from S and add it to L
             Alg(q)
             // Recurse
             Recurse()
             // Undo choice
             S = oldS
             L = oldL
             A = oldA
    }
    
    Alg(q){
         for i=1 to |V| {
              if (A(q,i)==1){
                   A(q,i)=0
              }
              for j=1 to |V| { 
                   if (A(j,i)==0){ 
                       k=k+1
                   } 
              } 
              if (k==|V|){ 
                  add i into S 
              }
         }
    }

I tried to execute the algorithm in order to understand it..

The set of starting nodes is: $S=\{b,e\}$.

The output set is $L=\{ \}$.

The adjacency matrix is the following: $$A:\begin{matrix}
& a & b & c & d & e & \\
- & - & - & - & - & - & \\
a & 0 & 0 & 1 & 1 & 0 & \\
b & 0 & 0 & 0 & 1 & 0 & \\
c & 0 & 0 & 0 & 0 & 0 & \\
d & 0 & 0 & 0 & 0 & 0 & \\
e & 1 & 0 & 0 & 0 & 0 &
\end{matrix}$$
Code: 
    Recurse() 
       oldA=A 
       oldS=S={b,e} 
       oldL=L={ } 
       q=b 
       S={e}, L{b} 
       Recurse() 
           oldA=A
           oldS=S={e} 
           oldL=L={b} 
           q=e 
           S={ }, L={b,e} 
           S={a} 
           Recurse() 
               oldA=A 
               oldS=S={a} 
               oldL=L={b,e} 
               q=a 
               S={ }, L={b,e,a} 
               S={c} 
               Recurse() 
                    oldA=A 
                    oldS=S={c} 
                    oldL=L={b,e,a} 
                    q=c 
                    S={ }, L=b,e,a,c} 
                    Recurse() 
                        output L={b,e,a,c}

But at the output set, node $d$ is missing. Have I done something wrong? (Thinking)
 
  • #17
evinda said:
But at the output set, node $d$ is missing. Have I done something wrong? (Thinking)

When you select q=a, not only node c is added to S, but node d should also be added to S. (Wasntme)
 
  • #18
I like Serena said:
When you select q=a, not only node c is added to S, but node d should also be added to S. (Wasntme)

I tried it again...

The set of starting nodes is: $S=\{b,e\}$.

The output set is $L=\{ \}$.

The adjacency matrix is the following: $$A:\begin{matrix}
& a & b & c & d & e & \\
- & - & - & - & - & - & \\
a & 0 & 0 & 1 & 1 & 0 & \\
b & 0 & 0 & 0 & 1 & 0 & \\
c & 0 & 0 & 0 & 0 & 0 & \\
d & 0 & 0 & 0 & 0 & 0 & \\
e & 1 & 0 & 0 & 0 & 0 &
\end{matrix}$$

Code: 
    Recurse() 
       oldA=A 
       oldS=S={b,e} 
       oldL=L={ } 
       q=b 
       S={e}, L{b} 
       Recurse() 
           oldA=A
           oldS=S={e} 
           oldL=L={b} 
           q=e 
           S={ }, L={b,e} 
           S={a} 
           Recurse() 
               oldA=A 
               oldS=S={a} 
               oldL=L={b,e} 
               q=a 
               S={ }, L={b,e,a} 
               S={c,d} 
               Recurse() 
                    oldA=A 
                    oldS=S={c,d} 
                    oldL=L={b,e,a} 
                    q=c 
                    S={d}, L={b,e,a,c} 
                    Recurse() 
                        olA=A 
                        oldS=S={d} 
                        oldL=L={b,e,a,c} 
                        q=d 
                        S={ }, L={b,e,a,c,d} 
                        Recurse() 
                            output L={b,e,a,c,d} 
                        S=oldS={d} 
                        L=oldL={b,e,a,c} 
                        A=oldA 
                        q=d 
                        S={ }, L={b,e,a,c,d} 
                        Recurse() 
                            output L={b,e,a,c,d}

Do we get the same result? Or have I set the wrong values at [m]S[/m], [m]L[/m], [m]A[/m] ? (Thinking)
 
  • #19
evinda said:
Do we get the same result? Or have I set the wrong values at [m]S[/m], [m]L[/m], [m]A[/m] ? (Thinking)

First node d was selected from S={d}.
After that, all selections from S={d} were complete.
Node d should not be selected a second time from the same S={d}. (Wasntme)
 
  • #20
I like Serena said:
First node d was selected from S={d}.
After that, all selections from S={d} were complete.
Node d should not be selected a second time from the same S={d}. (Wasntme)

So which should be the values of [m] S, L , A [/m] after the output [m]L={b,e,a,c,d}[/m]? :confused:
 
  • #21
evinda said:
So which should be the values of [m] S, L , A [/m] after the output [m]L={b,e,a,c,d}[/m]? :confused:

After that we first go back to S={d} and L={b,e,a,c}.
And since we've gone through all choices in S, we backtrack to S={c,d} and L={b,e,a}. (Thinking)
We've already had choice c, so the next choice from S is node d.
So we recurse and get to S={c} and L={b,e,a,d}.
And then we get to S={} and L={b,e,a,d,c}, which is the next solution. (Mmm)
 
  • #22
I like Serena said:
After that we first go back to S={d} and L={b,e,a,c}.
And since we've gone through all choices in S, we backtrack to S={c,d} and L={b,e,a}. (Thinking)
We've already had choice c, so the next choice from S is node d.
So we recurse and get to S={c} and L={b,e,a,d}.
And then we get to S={} and L={b,e,a,d,c}, which is the next solution. (Mmm)

I executed the algorithm...The set of starting nodes is: $S=\{b,e\}$.

The output set is $L=\{ \}$.

The adjacency matrix is the following: $$A:\begin{matrix}
& a & b & c & d & e & \\
- & - & - & - & - & - & \\
a & 0 & 0 & 1 & 1 & 0 & \\
b & 0 & 0 & 0 & 1 & 0 & \\
c & 0 & 0 & 0 & 0 & 0 & \\
d & 0 & 0 & 0 & 0 & 0 & \\
e & 1 & 0 & 0 & 0 & 0 &
\end{matrix}$$

Code: 
    Recurse() 
       oldA=A 
       oldS=S={b,e} 
       oldL=L={ } 
       q=b 
       S={e}, L{b} 
       Recurse() 
           oldA=A
           oldS=S={e} 
           oldL=L={b} 
           q=e 
           S={ }, L={b,e} 
           S={a} 
           Recurse() 
               oldA=A 
               oldS=S={a} 
               oldL=L={b,e} 
               q=a 
               S={ }, L={b,e,a} 
               S={c,d} 
               Recurse() 
                    oldA=A 
                    oldS=S={c,d} 
                    oldL=L={b,e,a} 
                    q=c 
                    S={d}, L={b,e,a,c} 
                    Recurse() 
                        olA=A 
                        oldS=S={d} 
                        oldL=L={b,e,a,c} 
                        q=d 
                        S={ }, L={b,e,a,c,d} 
                        Recurse() 
                            output L={b,e,a,c,d} 
                        S=oldS={d} 
                        L=oldL={b,e,a,c} 
                        A=oldA 
                    S=oldS={c,d} 
                    L=oldL={b,e,a} 
                    A=oldA 
                    q=d 
                    S={c}, L={b,e,a,d} 
                    Recurse() 
                        oldA=A 
                        oldS=S={c} 
                        oldL=L={b,e,a,d} 
                        q=c 
                        S={ }, L={b,e,a,d,c} 
                        Recurse() 
                             output L={b,e,a,d,c} 
                        S=oldS={c} 
                        L=oldL={b,e,a,d} 
                        A=oldA 
                    S=oldS={c,d} 
                    L=oldL={b,e,a} 
                    A=oldA 
               S=oldS={a} 
               L=oldL={b,e} 
               A=oldA 
           S=oldS={e} 
           L=oldL={b} 
           A=oldA 
       S=oldS={b,e} 
       L=oldL={ } 
       A=oldA 
       q=e 
       S={b,a}, L={e} 
       Recurse() 
            oldA=A 
            oldS=S={b,a} 
            oldL=L={e} 
            q=b 
            S={a}, L={e,b} 
            Recurse() 
               oldA=A 
               oldS=S={a} 
               oldL=L={e,b} 
               q=a 
               S={ }, L={e,b,a} 
               S={c,d} 
               Recurse() 
                    oldA=A 
                    oldS=S={c,d} 
                    oldL=L={e,b,a} 
                    q=c 
                    S={d}, L={e,b,a,c} 
                    Recurse() 
                        olA=A 
                        oldS=S={d} 
                        oldL=L={e,b,a,c} 
                        q=d 
                        S={ }, L={e,b,a,c,d} 
                        Recurse() 
                            output L={e,b,a,c,d} 
                        S=oldS={d} 
                        L=oldL={e,b,a,c} 
                        A=oldA 
                    S=oldS={c,d} 
                    L=oldL={e,b,a} 
                    A=oldA 
                    q=d 
                    S={c}, L={e,b,a,d} 
                    Recurse() 
                        oldA=A 
                        oldS=S={c} 
                        oldL=L={e,b,a,d} 
                        q=c 
                        S={ }, L={e,b,a,d,c} 
                        Recurse() 
                             output L={e,b,a,d,c} 
                        S=oldS={c} 
                        L=oldL={e,b,a,d} 
                        A=oldA 
                    S=oldS={c,d} 
                    L=oldL={e,b,a} 
                    A=oldA 
               S=oldS={a} 
               L=oldL={e,b} 
               A=oldA 
           S=oldS={b,a} 
           L=oldL={e} 
           A=oldA 
           q=a 
           S={b}, L={e,a} 
           S={b,c} 
           Recurse() 
               oldA=A 
               oldS=S={b,c} 
               oldL=L={e,a} 
               q=b 
               S={c}, L={e,a,b} 
               S={c,d} 
               Recurse() 
                      oldA=A 
                      oldS=S={c,d} 
                      oldL=L={e,a,b} 
                      q=c 
                      S={d}, L={e,a,b,c} 
                      Recursive() 
                            oldA=A 
                            oldS=S={d} 
                            oldL=L={e,a,b,c} 
                            q=d 
                            S={ }, L={e,a,b,c,d} 
                                Recurse() 
                                     output L={e,a,b,c,d} 
                                S=oldS={d} 
                                L=oldL={e,a,b,c} 
                                A=oldA 
                      S=oldS={c,d} 
                      L=oldL={e,a,b} 
                      A=oldA 
                      q=d 
                      S={c}, L={e,a,b,d} 
                      Recursive() 
                            oldA=A 
                            oldS=S={c} 
                            oldL=L={e,a,b,d} 
                            q=c 
                            S={ }, L={e,a,b,d,c} 
                            Recurse() 
                                  output L={e,a,b,d,c} 
                            S=oldS={c} 
                            L=oldL={e,a,b,d} 
                            A=oldA  

                    ......

I found all the topological sortings also by hand and I found only 3. Is it right that we have found so many topological sortings so far with the algorithm? (Thinking)
 
  • #23
evinda said:
I found all the topological sortings also by hand and I found only 3. Is it right that we have found so many topological sortings so far with the algorithm? (Thinking)

I think the possible topological sortings are:
  1. beacd
  2. beadc
  3. ebacd
  4. ebadc
  5. eabcd
  6. eabdc
  7. eacbd
(Thinking)
 
  • #24
I like Serena said:
I think the possible topological sortings are:
  1. beacd
  2. beadc
  3. ebacd
  4. ebadc
  5. eabcd
  6. eabdc
  7. eacbd
(Thinking)

In order to find the possible topological sortings, don't we apply Depth-first search and write the nodes in decreasing order as for the finishing times? (Thinking)
 
  • #25
evinda said:
In order to find the possible topological sortings, don't we apply Depth-first search

Yes. (Nod)

and write the nodes in decreasing order as for the finishing times? (Thinking)

Huh? :confused:
We process the nodes in alphabetical order, which is the first solution as far as that is possible.
Then we recurse to find the other solutions. (Wasntme)
 
  • #26
I like Serena said:
Yes. (Nod)
Huh? :confused:
We process the nodes in alphabetical order, which is the first solution as far as that is possible.
Then we recurse to find the other solutions. (Wasntme)

I found this: http://www.cse.ust.hk/faculty/golin/COMP271Sp03/Notes/MyL08.pdf and according to the page 13, the idea of Topological Sorting is the following:

Run the DFS on the DAG and output the vertices in reverse order of finishing time.

When we do it like that, don't we get only three possible topologicsl sortings? :confused:
I got the following: [m]{b,e,a,d,c}, {b,e,a,c,d}, {e,a,c,b,d} [/m]..
 
  • #27
evinda said:
I found this: http://www.cse.ust.hk/faculty/golin/COMP271Sp03/Notes/MyL08.pdf and according to the page 13, the idea of Topological Sorting is the following:

Run the DFS on the DAG and output the vertices in reverse order of finishing time.

When we do it like that, don't we get only three possible topologicsl sortings? :confused:
I got the following: [m]{b,e,a,d,c}, {b,e,a,c,d}, {e,a,c,b,d} [/m]..

But... isn't for instance [m]{e,b,a,c,d}[/m] a valid topological sorting? (Thinking)
 
  • #28
I like Serena said:
But... isn't for instance [m]{e,b,a,c,d}[/m] a valid topological sorting? (Thinking)

After one node can't we only have an adjacent node of this node? Or am I wrong?
I thought that after [m] e [/m], the only node that can appear is the node [m] a [/m]... (Thinking)
 
  • #29
evinda said:
After one node can't we only have an adjacent node of this node? Or am I wrong?
I thought that after [m] e [/m], the only node that can appear is the node [m] a [/m]... (Thinking)

(Wait) That what I said doesn't hold.. If we find at a topological sorting a node after an other, the latter doesn't have to be adjacent to the first one..
But we should have to add an other condition so that we get only the right three possible topological sorting, but I can't think of one..
Do you maybe have an idea? (Thinking)
 
  • #30
evinda said:
(Wait) That what I said doesn't hold.. If we find at a topological sorting a node after an other, the latter doesn't have to be adjacent to the first one..
But we should have to add an other condition so that we get only the right three possible topological sorting, but I can't think of one..
Do you maybe have an idea? (Thinking)

Wikipedia is currently not responding, but from mathworld.wolfram I have:
A topological sort is a permutation p of the vertices of a graph such that an edge {i,j} implies that i appears before j in p (Skiena 1990, p. 208).​

The sorting I gave fulfills the conditions of that definition.
So I really think there are 7 topological sortings. (Thinking)

EDIT: Wait! (Wait) Wikipedia is responding now. It says:
In computer science, a topological sort (sometimes abbreviated topsort or toposort) or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. ​
Anyway, it's the same thing. (Worried)
 
  • #31
I like Serena said:
Wikipedia is currently not responding, but from mathworld.wolfram I have:
A topological sort is a permutation p of the vertices of a graph such that an edge {i,j} implies that i appears before j in p (Skiena 1990, p. 208).​

The sorting I gave fulfills the conditions of that definition.
So I really think there are 7 topological sortings. (Thinking)

EDIT: Wait! (Wait) Wikipedia is responding now. It says:
In computer science, a topological sort (sometimes abbreviated topsort or toposort) or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. ​
Anyway, it's the same thing. (Worried)
In my book, there is the following algorithm:

Code: 
TOPOLOGICAL-SORT(G)    
    1.  call DFS(G) to compute finishing times v.f for each vertex v    
    2.  as each vertex is finished, insert it onto the front of a linked list 
    3.  return the linked list of vertices
https://www.dropbox.com/s/d1ucdvokx...troduction_to_algorithms_3rd_edition.pdf?dl=0
 
  • #32
Wouldn't that algorithm return just 1 solution? (Wondering)
 
  • #33
I like Serena said:
Wouldn't that algorithm return just 1 solution? (Wondering)

Yes, it would.. But DFS doesn't always return the same result. If we apply for example twice the DFS at a graph and at one step, there are two different nodes to visit, we can once visit firstly the first node and the second time when we apply the algorithm we would visit firstly the second node and so the results would be different, since the finishing times would be different.For example if we have this graph:View attachment 4263

applying DFS we could get these discovery and finishing times:View attachment 4264these ones:View attachment 4265

or these ones:

View attachment 4266So at the first case, the result of the topological sorting would be: {b, e, a, d, c}, at the second case the result would be: { b, e, a, c, d} and at the third case: {e, a, c, b, d}.How could an algorithm return all these possible results of topological sorting?
 

Attachments

  • grap.png
    grap.png
    2.9 KB · Views: 67
  • grap1.png
    grap1.png
    4.5 KB · Views: 60
  • grap2.png
    grap2.png
    4.5 KB · Views: 62
  • grap3.png
    grap3.png
    4.3 KB · Views: 69
  • #34
I don't understand. (Sweating)

What do your arrows and your numbers mean? (Wondering)
 
  • #35
I like Serena said:
I don't understand. (Sweating)

What do your arrows and your numbers mean? (Wondering)

The numbers respresent the discovery and finishing times. The arrows show from which node we came to the current one.I applied only DFS, starting with the nodes that have no incoming edges. (Tmi)

Now I got the following topological sortings:

[m] {e, b, a, d, c}, {b, a, a, d, c}, {b, e, a, c, d}, {e, b, a, c, d}, {e, a, c, b, d}, {e, a, b, d, c}[/m]

But I haven't found the topological sorting [m] {e, a, b, c, d}[/m].. How do we get it? (Thinking)
To find this, we should start from the node [m]d [/m], or not?
 

Similar threads

MHB Topological Sort: Finding a Contradiction
Replies
2
Views
2K
MHB Merging $k$ Sorted Lists with a Thin Heap: A $\mathcal{O}(n \lg k)$ Algorithm
Replies
1
Views
1K
MHB Find Algorithm for O(V*E) Transitive Closure of a Graph
Replies
11
Views
3K
Python Is it possible to simulate gravitational waves using python?
Replies
8
Views
3K
MHB Explaining Time Complexity and NP Problems
Replies
17
Views
4K
MHB Does Max-Kruskal Algorithm Find the Maximum Spanning Tree?
Replies
1
Views
1K
MHB What Determines the Running Time of Kruskal's Algorithm?
Replies
1
Views
1K
MHB Finding a Local Minimum of $G$: Algorithm & Analysis
Replies
22
Views
5K
MHB How to Multiply Two Polynomials Using Divide-and-Conquer Algorithms?
Replies
1
Views
1K
MHB Find total number of republications
Replies
22
Views
1K

Hot Threads

Recent Insights

Back
Top