Alternative method of finding Electric flux from non-uniform field

[ChiralSuperfields]

Homework Statement

Please see below

Relevant Equations

Electric flux formula (please see below)

For this problem,

The solution is,

However, why can the differential area not be:

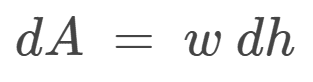
I tried integrating and got,

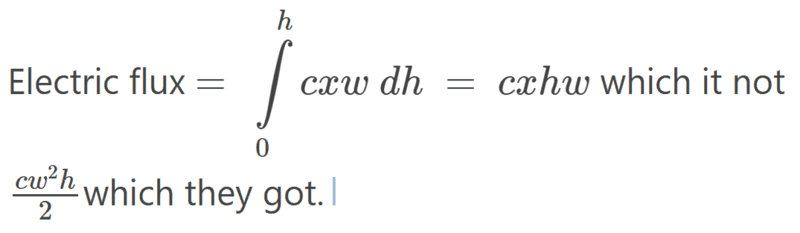
Can someone please tell me what I have done wrong?

Thank you!

 

[kuruman]

First of all $\hat k\cdot \hat k=1$, not zero. I think they meant to say $\hat i\cdot \hat k=0$ which is correct. The differential area is $dA=dx~dy.$ It cannot be $dA=wdh$ because $h$ is constant. Have you been taught double integration?

 

[ChiralSuperfields]

First of all $\hat k\cdot \hat k=1$, not zero. I think they meant to say $\hat i\cdot \hat k=0$ which is correct. The differential area is $dA=dx~dy.$ It cannot be $dA=wdh$ because $h$ is constant. Have you been taught double integration?

Thank you @kuruman ! No sorry I have not been taught double integration yet. Is this differential area, correct?

It seems that I get the same result as above when I incorrectly used the dh. I think it something to do with the x?

 

[haruspex]

Thank you @kuruman ! No sorry I have not been taught double integration yet. Is this differential area, correct?

View attachment 320026
It seems that I get the same result as above when I incorrectly used the dh. I think it something to do with the x?

Since x is a variable across the integration area, it cannot appear in the answer.
A general fact in Cartesian coordinates is dA=dx.dy, and to integrate over an area you have to integrate wrt each. You can do the integration in either order.
In the present case, the function being integrated is a function of x only. That makes the integration wrt y trivial: $\int_{x=0}^{w}\int_{y=0}^h f(x).dy.dx=\int_{x=0}^{w}h f(x).dx$.
You method fails because $\int_{x=0}^{w} f(x).dx\neq wf(x)$. Indeed, that would be a nonsense because $\int_{x=0}^{w} f(x).dx$ is not a function of a variable x.

 

[PhDeezNutz]

Part 1

Only the $z$ component of the field (which is dependent on $x$) will produce flux through said sheet.

If you are not familiar with double integration let’s find a work around

Part 2

Can you find the “flux” through the infinitesimally small sliver that straddles the x-axis (I.e. y = 0)?

Part 3

Now look at the other slivers that comprises the area (other $y = constant$ slivers). Given the expression for the field do you expect these flux values to change for subsequent slivers after the sliver flux found in part 2?

If not how would you take your answer from part 2 and apply it to the whole plane in question?

 

[nasu]

Thank you @kuruman ! No sorry I have not been taught double integration yet. Is this differential area, correct?

View attachment 320026
It seems that I get the same result as above when I incorrectly used the dh. I think it something to do with the x?

You can take advantage of the fact that the component of the electric field along z (the only one that matters) depends only on x (and not y). So you can divide the area into strips along the y-axis, of area dA=h dx. They all have the same value of the field as they have the same value of x. The integral should be on the variable x as the field depends on x. This type of "shortcut" is used a lot in introductory courses so you don't need to know multivariable calculus to solve the problem. Even though it results from the double integral, as shown by kuruman.

 

[ChiralSuperfields]

Thank you @haruspex , @PhDeezNutz and @nasu for your replies!