Ampere's Law Problem: B-Field from a Current Distribution

[Physicslearner500039]

Homework Statement

In a particular region there is a uniform current density of 15 A/m2 in the positive z direction. What is the value of ~ B· d'S when that line integral is calculated along the three straight-line segments from (x, y, z) coordinates (4d,0,0) to (4d, 3d, 0) to (0, 0, 0) to (4d, 0, 0),where d = 20 cm?

Relevant Equations

No equations available

This is the problem, first time i am attempting the Ampere's law problem

From the above question this is my attempt, the picture is

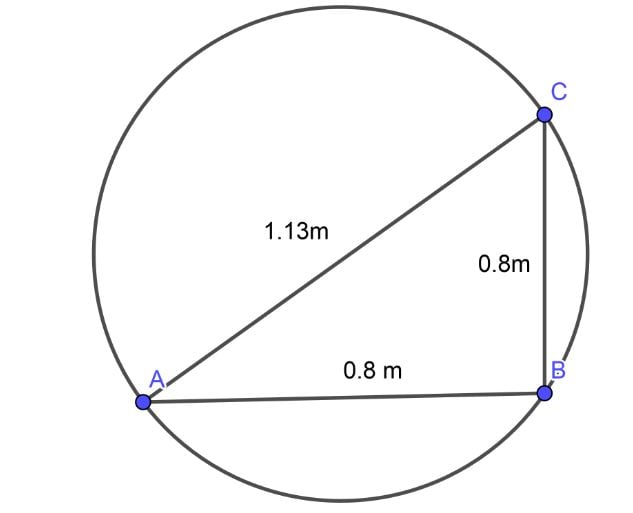
∫B.ds = μ*Ienc; ----> Ampere law , where Ienc is the current enclosed in the amperian loop.
I assume the circle as the amperian loop, is it correct? Can i choose cylinder also?
I am not sure but i ended up doing this,
Ienc = 15 * 0.5*0.8*0.8 (Area of triangle * current) = 4.8 Amps
∫B.ds = μ*4.8 = 4*π*4.8 *10^-7 = 60.3*10^-7; Is it correct? Please advise.

 

[BvU]

Righthand side is $3d$, not $4d$

 

[Physicslearner500039]

Sorry my mistake the updated figure and the calculations are

The calculations are
Ienc = 15*0.5*0.8*0.6= 3.6 amps
∫B.ds = μ*3.6 = 4*π*3.6*10^-7 = 4.5*10^-6

 

[BvU]

Is it correct? Please advise.

PF isn't for stamp-approving homework -- we ask, guide and advise. You want to convince yourself that what you found is correct. Your own responsibility !

In this case, if I were to grade this and it's a physics class, I wouldn't give full marks for an answer without the dimension -- but then I wouldn't ask for a value either.

 

[kuruman]

For full marks, I would also be looking for justification why you chose to substitute +3.6 A as opposed to -3.6 A in your equation.

 

[Physicslearner500039]

Yes I am trying to understand the Amperes better. This is one of the doubts i have about it. In the diagram

from the book the loop which was considered as amperian loop, the net current is i1-i2, but my doubt is the one, i have highlighted as yellow (i could not color it perfectly) there is no current there, am I correct? Then why should it be i1-i2?

As another example

The one again i colored as Yellow there is no current. The current is only inside the wire then why should i say the current is enclosed in the complete amperian loop? Please advise.

 

[kuruman]

Look at the picture below. How many houses are enclosed by the circular street? I count 16. Does the central empty space make a difference to the number of houses enclosed by the street? Although it is true that one can build more houses within that space, the number of houses enclosed by this street in this picture is 16. What isn't there, doesn't count.

The same applies to currents enclosed by Amperian loops. The fact that you don't have any current flowing through some part of the loop does not affect the fact that you have +i₁ and -i₂ through other parts of the loop. Formally adding all these to get the total enclosed current gives $$i_{encl.}=+i_1+(-i_2)+0$$where the zero takes into account what is flowing through the yellow areas, namely nothing. See how it works?