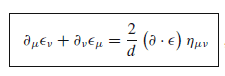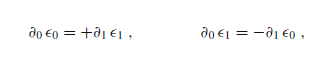SUMMARY
The discussion focuses on an elementary equation manipulation in 2-dimensional conformal field theory (CFT), specifically addressing the relationship between the left-hand side (LHS) and right-hand side (RHS) of an equation involving the metric and the Kronecker symbol. Participants clarify that setting indices μ and ν to 0 and 1 leads to confusion regarding the equality of LHS and RHS. The correct interpretation involves recognizing that ∂⋅ε represents a sum of components, leading to the conclusion that 2∂0ε0 equals ∂0ε0 plus ∂1ε1 for the 00 component.
PREREQUISITES
- Understanding of 2-dimensional conformal field theory (CFT)
- Familiarity with the Kronecker delta and its application in tensor calculations
- Knowledge of partial derivatives and their notation in mathematical physics
- Basic grasp of metric tensors in Euclidean space
NEXT STEPS
- Study the properties of the Kronecker delta in tensor analysis
- Learn about the implications of metric tensors in conformal field theories
- Explore the concept of inner products in the context of vector fields
- Investigate the role of partial derivatives in higher-dimensional field theories
USEFUL FOR
This discussion is beneficial for theoretical physicists, particularly those specializing in conformal field theory, as well as students and researchers looking to deepen their understanding of tensor manipulations and metric properties in physics.