- #1
- 3,149
- 8
It is assumed that the reader is familiar with the basic concepts of structural analysis. Further on, I am aware of the possible inconsistencies and errors in this writing, and hereby invite all who have comments and objections to contribute and help to make this small tutorial useful for anybody interested in the analysis of statically indeterminate systems.
1. THE FORCE METHOD.
1.1. INTRODUCTION THROUGH AN EXAMPLE.
Perhaps the most standard example of the force method application is the system in Figure 1. It is obvious that the system's degree of statical indeterminacy equals one, since the number of constraints equals 4, and the number of equations of equilibrium we can use equals 3. Note that, if we removed the roller support at point B, we would be left with a statically determinate console with a support at point A, which (the support) represents three kinematic constraints. Hence, we can refer to the support at point B as a statical constraint, since the system, after having this support removed, still remains geometrically stable (i.e. it does NOT become a mechanism).
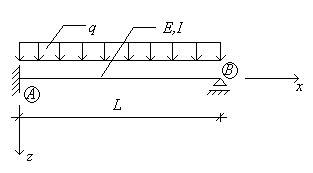
Figure 1.
The geometrical and material characteristics are all displayed in Figure 1. The module of elasticity equals E, and it is constant along the whole length L, as is the moment of inertia of the cross section, denoted by I (with respect to the y-axis, which is pointing 'towards us').
Let us remove the roller support at point B, and 'replace it' with its reactive force [itex]R_{B}[/itex]. We shall explicitely use the equations of equilibrium for the z-direction (1), and we shall set the sum of the torques with respect to point A to equal zero (2):
(1)
[tex]\sum F_{z} = 0 \rightarrow R_{A} + R_{B} = qL \ \text{,}[/tex]
(2)
[tex]\sum M_{A} = 0 \rightarrow M_{A} + R_{B}L = \frac{qL^2}{2} \ \text{,}[/tex]
where [itex]M_{A}[/itex] is the reaction torque at point A, [itex]R_{A}[/itex] the reaction force in the z-direction at the same point, and [itex]R_{B}[/itex] the reaction force in the same direction at point B. (It is assumed that the positive direction of the torques is counter-clockwise, and the positive direction of the vertical forces is in the positive direction of the z-axis).
It is obvious that the system of two equations (1) and (2), which represents the conditions of equilibrium of the system, has no unique solution, since we are left with two equations and three unknowns, [itex]M_{A}[/itex], [itex]R_{A}[/itex] and [itex]R_{B}[/itex]. Further on, we can write the system of equations in the form:
(1')
[tex]R_{A} = qL - R_{B}[/tex]
(2')
[tex]M_{A} = \frac{qL^2}{2} - R_{B}L \ \text{.}[/tex]
Now we can see the the equations of equilibrium will be satisfied for any value of the reaction [itex]R_{B}[/itex], i.e. the system has a one-parameter solution, where the parameter is [itex]R_{B}[/itex]. This means that there is an infinite number of equilibrium states of the system. But, the one we are trying to find is the one which satisfies the displacement conditions of the system - i.e. the vertical displacement at point B equals zero, since, in the original system there exists a support at point B which prevents a vertical displacement at that point.
The vertical displacement of the point B has two contributions: one comes from the load q, and the other from the reactive force [itex]R_{B}[/itex] acting at that point. So, it can be expressed as the superposition of these two contributions, respectively:
[tex]w_{B} = \frac{qL^4}{8EI} - R_{B}\frac{L^3}{3EI} \ \text{.}[/tex]
(Note that the displacement of the reactive force [itex]R_{B}[/itex] has a negative sign, since the force is assumed to point in the negative direction of the z-axis.) As mentioned, the displacement must equal zero, which represents the additional condition we need to describe the desired 'real' state of equilibrium of the system, so [itex]w_{B} = 0[/itex] (3) implies:
[tex]R_{B} = \frac{3}{8}qL \ \text{.}[/tex]
Now we can finally solve equations (1') and (2'), i.e. calculate the reactive forces [itex]R_{A}[/itex] and [itex]M_{A}[/itex], and, of course, solve standard statics problems as before - find bending moment and shear force diagrams, displacements, etc.
The provided example was supposed to serve as a brief introduction to the force method, whose summary can easily be distinguished from the very same example. First, a support, which represents a statical constraint is removed and replaced with a reactive force in the 'position and direction' of the support. Further on, the equations of equilibrium are set up. Finally,a kinematic condition (a condition of displacement, i.e. a geometric condition) is set up to determine which state of equilibrium is the real one. As a final illustraion, one can find deflection curves for some values of [itex]R_{B}[/itex] which do not satisfy the condition (3) in Figure 2, while Figure 3 represents the actual deflection curve of the bar, which is in consistence with the condition (3). (The console is placed on the horizontal axis, and the diagrams are plotted for L = 5. The vertical axis represents the vertical displacement w.)
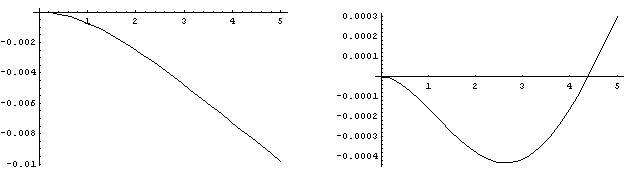
Figure 2.
In the end, it is of great importance to mention that this rough illustration of the force method concept applies to systems with more than one degree of statical indeterminacy - in general, for a statically indeterminate system with the degree of statical indeterminacy n, one merely has to pick n different supports (i.e. statical constraints) and replace them with forces acting in the points and the directions of the supports. Of course, this system, which is referred to as the primary system, is not allowed to be a mechanism, which means we can not remove just any support as we wish. In our example, we could as well add a hinge to point A, which physically means we have removed the part of the rigid support which transfers torques. After that, we would have to add a torque M to that point, and that torque should satisfy condition equivalent to (3), which would state that the rotation at point A should equal zero. In general, when dealing with statically indeterminate systems with a degree of statical indeterminacy equal to n, we have n displacement conditions (in our case we have only one - equation (3) ).
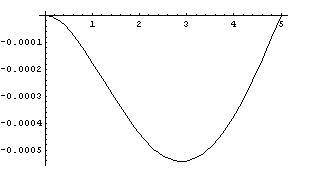
Figure 3.
A more detailed and formal outline of the force method shall be introduced in section 1.2.
1. THE FORCE METHOD.
1.1. INTRODUCTION THROUGH AN EXAMPLE.
Perhaps the most standard example of the force method application is the system in Figure 1. It is obvious that the system's degree of statical indeterminacy equals one, since the number of constraints equals 4, and the number of equations of equilibrium we can use equals 3. Note that, if we removed the roller support at point B, we would be left with a statically determinate console with a support at point A, which (the support) represents three kinematic constraints. Hence, we can refer to the support at point B as a statical constraint, since the system, after having this support removed, still remains geometrically stable (i.e. it does NOT become a mechanism).
Figure 1.
The geometrical and material characteristics are all displayed in Figure 1. The module of elasticity equals E, and it is constant along the whole length L, as is the moment of inertia of the cross section, denoted by I (with respect to the y-axis, which is pointing 'towards us').
Let us remove the roller support at point B, and 'replace it' with its reactive force [itex]R_{B}[/itex]. We shall explicitely use the equations of equilibrium for the z-direction (1), and we shall set the sum of the torques with respect to point A to equal zero (2):
(1)
[tex]\sum F_{z} = 0 \rightarrow R_{A} + R_{B} = qL \ \text{,}[/tex]
(2)
[tex]\sum M_{A} = 0 \rightarrow M_{A} + R_{B}L = \frac{qL^2}{2} \ \text{,}[/tex]
where [itex]M_{A}[/itex] is the reaction torque at point A, [itex]R_{A}[/itex] the reaction force in the z-direction at the same point, and [itex]R_{B}[/itex] the reaction force in the same direction at point B. (It is assumed that the positive direction of the torques is counter-clockwise, and the positive direction of the vertical forces is in the positive direction of the z-axis).
It is obvious that the system of two equations (1) and (2), which represents the conditions of equilibrium of the system, has no unique solution, since we are left with two equations and three unknowns, [itex]M_{A}[/itex], [itex]R_{A}[/itex] and [itex]R_{B}[/itex]. Further on, we can write the system of equations in the form:
(1')
[tex]R_{A} = qL - R_{B}[/tex]
(2')
[tex]M_{A} = \frac{qL^2}{2} - R_{B}L \ \text{.}[/tex]
Now we can see the the equations of equilibrium will be satisfied for any value of the reaction [itex]R_{B}[/itex], i.e. the system has a one-parameter solution, where the parameter is [itex]R_{B}[/itex]. This means that there is an infinite number of equilibrium states of the system. But, the one we are trying to find is the one which satisfies the displacement conditions of the system - i.e. the vertical displacement at point B equals zero, since, in the original system there exists a support at point B which prevents a vertical displacement at that point.
The vertical displacement of the point B has two contributions: one comes from the load q, and the other from the reactive force [itex]R_{B}[/itex] acting at that point. So, it can be expressed as the superposition of these two contributions, respectively:
[tex]w_{B} = \frac{qL^4}{8EI} - R_{B}\frac{L^3}{3EI} \ \text{.}[/tex]
(Note that the displacement of the reactive force [itex]R_{B}[/itex] has a negative sign, since the force is assumed to point in the negative direction of the z-axis.) As mentioned, the displacement must equal zero, which represents the additional condition we need to describe the desired 'real' state of equilibrium of the system, so [itex]w_{B} = 0[/itex] (3) implies:
[tex]R_{B} = \frac{3}{8}qL \ \text{.}[/tex]
Now we can finally solve equations (1') and (2'), i.e. calculate the reactive forces [itex]R_{A}[/itex] and [itex]M_{A}[/itex], and, of course, solve standard statics problems as before - find bending moment and shear force diagrams, displacements, etc.
The provided example was supposed to serve as a brief introduction to the force method, whose summary can easily be distinguished from the very same example. First, a support, which represents a statical constraint is removed and replaced with a reactive force in the 'position and direction' of the support. Further on, the equations of equilibrium are set up. Finally,a kinematic condition (a condition of displacement, i.e. a geometric condition) is set up to determine which state of equilibrium is the real one. As a final illustraion, one can find deflection curves for some values of [itex]R_{B}[/itex] which do not satisfy the condition (3) in Figure 2, while Figure 3 represents the actual deflection curve of the bar, which is in consistence with the condition (3). (The console is placed on the horizontal axis, and the diagrams are plotted for L = 5. The vertical axis represents the vertical displacement w.)
Figure 2.
In the end, it is of great importance to mention that this rough illustration of the force method concept applies to systems with more than one degree of statical indeterminacy - in general, for a statically indeterminate system with the degree of statical indeterminacy n, one merely has to pick n different supports (i.e. statical constraints) and replace them with forces acting in the points and the directions of the supports. Of course, this system, which is referred to as the primary system, is not allowed to be a mechanism, which means we can not remove just any support as we wish. In our example, we could as well add a hinge to point A, which physically means we have removed the part of the rigid support which transfers torques. After that, we would have to add a torque M to that point, and that torque should satisfy condition equivalent to (3), which would state that the rotation at point A should equal zero. In general, when dealing with statically indeterminate systems with a degree of statical indeterminacy equal to n, we have n displacement conditions (in our case we have only one - equation (3) ).
Figure 3.
A more detailed and formal outline of the force method shall be introduced in section 1.2.
Last edited by a moderator: