CGandC
- 326
- 34
I have a question regarding a theoretical analysis of Ultrasonic waves :
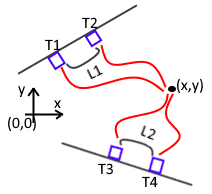
The next picture represents a system of transducers sitting on fixed boards:
Datum:
* there are 4 transducers ( represented by blue color , indexed by letter ' T ' ) , each outputting Ultrasonic wave (represented by red) and sitting on planar surfaces
* 2 transducers are separated with distance L1 from each other
* another 2 transducers are separated with distance L2 from each other
Question:
How can I describe the interference and Intensity of the Ultrasonic waves ( from each transducer ) at a point (x,y) in space? What's the mathematical/theoretical formalism?
Note: I didn't write frequencies/wavelengths/pressure magnitude ,etc. These will be variables ( not necessarily to be found )
The next picture represents a system of transducers sitting on fixed boards:
Datum:
* there are 4 transducers ( represented by blue color , indexed by letter ' T ' ) , each outputting Ultrasonic wave (represented by red) and sitting on planar surfaces
* 2 transducers are separated with distance L1 from each other
* another 2 transducers are separated with distance L2 from each other
Question:
How can I describe the interference and Intensity of the Ultrasonic waves ( from each transducer ) at a point (x,y) in space? What's the mathematical/theoretical formalism?
Note: I didn't write frequencies/wavelengths/pressure magnitude ,etc. These will be variables ( not necessarily to be found )