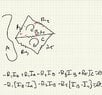guyvsdcsniper
- 264
- 37
- Homework Statement
- Use the loop current method on bridge circuit to generate 3 loop equations
- Relevant Equations
- Kirchoff's law
Attached is the example I am working out of a textbook that involves using the Loop Current Method on a bridge circuit. In the pictures attached I am following section 1.6.2 which produces loop equations (1.24) for figure 1.9. Figure 1.7 provides the direction of current.
I am having trouble producing the same result as the book I am using for Loop B and C.
Following Loop A, we travel up the EMF,
##\varepsilon##, and then we reach ##R_1##. At this resistor, ##I_a## travels down the resistor and ##I_b## travels up it. Likewise, at ##R_3## ##I_a## travels down the resistor and ##I_c## travels up it. Traveling down the resistor leads to a drop in voltage which leads to a negative sign in associated with that voltage.
Following this logic, I receive the same equation for Loop A as seen in equation 1.24.
So now when evaluating Loop B, I will begin at Node 4. Again, at ##R_1## ##I_a## travels down the resistor and ##I_b## travels up it. This produces ##R_1I_b-R_1I_a##. Next we go down resistor ##R_2## and get ##-R_2I_b##. Finally we have resistor ##R_5##. ##I_b## travels up and ##I_c## travels down this resistor, giving ##R_5I_b-R_5I_c##. Simplifying this and setting it equal to zero gives:
$$-R_1[I_a-I_b]-R_2I_b-R_5[I_c-I_b]=0$$.
So my logic works for Loop A but for Loop B, this logic produces the opposite of what the book gives for the resistors that contain a superposition of current.
Could someone help me understand how I am approaching this wrong?
I am having trouble producing the same result as the book I am using for Loop B and C.
Following Loop A, we travel up the EMF,
##\varepsilon##, and then we reach ##R_1##. At this resistor, ##I_a## travels down the resistor and ##I_b## travels up it. Likewise, at ##R_3## ##I_a## travels down the resistor and ##I_c## travels up it. Traveling down the resistor leads to a drop in voltage which leads to a negative sign in associated with that voltage.
Following this logic, I receive the same equation for Loop A as seen in equation 1.24.
So now when evaluating Loop B, I will begin at Node 4. Again, at ##R_1## ##I_a## travels down the resistor and ##I_b## travels up it. This produces ##R_1I_b-R_1I_a##. Next we go down resistor ##R_2## and get ##-R_2I_b##. Finally we have resistor ##R_5##. ##I_b## travels up and ##I_c## travels down this resistor, giving ##R_5I_b-R_5I_c##. Simplifying this and setting it equal to zero gives:
$$-R_1[I_a-I_b]-R_2I_b-R_5[I_c-I_b]=0$$.
So my logic works for Loop A but for Loop B, this logic produces the opposite of what the book gives for the resistors that contain a superposition of current.
Could someone help me understand how I am approaching this wrong?