Analyzing Electromagnetic Forces in a Two-Sphere System with Insulating Fiber

In summary, two small plastic spheres with a mass of 0.1g each are arranged on an insulating fiber with identical positive charges. One sphere is resting against a knot while the other is 6 cm away from the knot. Using Coulomb's Law, the electric force between the spheres can be calculated. To keep the higher bead from moving further than 6 cm, another force is needed. Further analysis is required to determine this force.
  • #1
Drain Brain
144
0
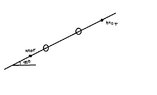
the two small plastic spheres are arranged so that they can slide freely along the insulating fiber. Each has a mass of 0.1g. The spheres are given identical positive charges. a. If the lower sphere is resting against the lower knot while the upper sphere moves to a location 6 cm distant from that knot, find the charge on each. b. if the charges remain the same, what angle should the fiber make with the horizontal to double the separation?

can you help on this problem. I'm having a hard time analyzing it. There's no given force(repulsive) I can't seem to use coulombs law here. please help!
 

Attachments

  • emags.jpg
    emags.jpg
    11.2 KB · Views: 64
Mathematics news on Phys.org
  • #2
Each of the plastic spheres repels the other, since they are both positively charged-this is why one of the spheres moves 6 cm up the fiber. Therefore, the third-law pair here is electric force with electric force, and you can use Coulomb's Law.
We also need another force, one that keeps the higher bead from moving away further than 6 cm. So, what do you think you should do now?
 

FAQ: Analyzing Electromagnetic Forces in a Two-Sphere System with Insulating Fiber

What is electromagnetism?

Electromagnetism is the branch of physics that studies the relationship between electricity and magnetism. It describes how electrically charged particles interact with each other and with magnetic fields.

How is electromagnetism used in everyday life?

Electromagnetism is used in a wide range of everyday devices, such as cell phones, computers, and televisions. It is also used in power generation and transportation systems.

What is the difference between electricity and magnetism?

Electricity is the flow of electric charge, while magnetism is the force that results from the motion of electric charges. In other words, electricity produces magnetism and magnetism can produce electricity.

How do you solve an electromagnetics problem?

To solve an electromagnetics problem, you must first understand the principles and equations of electromagnetism. Then, you can use mathematical and computational methods to analyze the problem and find a solution.

What are some real-world applications of electromagnetism?

Some real-world applications of electromagnetism include electric motors, generators, transformers, and MRI machines. It also plays a crucial role in wireless communication technologies such as radio, television, and cellular networks.

Similar threads

A neutral conducting sphere and an insulating sphere....
Replies
8
Views
3K
Calculating the number of electrons given the force of repulsion
Replies
5
Views
3K
How do I calculate the force between a charged and a neutral sphere
Replies
5
Views
2K
Analyzing the Force of Two Disk Magnets on a Metal Plate
Replies
2
Views
1K
Finding the charge on two beads?
Replies
8
Views
2K
Can the Sphere of Radius 'a' Be Modeled as a Point Particle?
Replies
2
Views
4K
Energy in system of two conducting spheres
Replies
5
Views
2K
Without integrating, show two metal spheres collide in <425s
Replies
3
Views
1K
Homework help:A small plastic sphere with a mass of 2.60 X 10-15 kg
Replies
5
Views
4K
Analyzing Forces & Electrons: Free Body Diagram
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top