Angular acceleration and moment of inertia on a pulley

[cloudboy]

Homework Statement

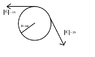
Two forces are applied to a pulley with a moment of inertia I = .15kg*m^2.
The pulley is mounted so that its frictionless axle is fixed in place.

1) What is the angular acceleration of the pulley?

2) If the pulley starts from rest, how long does it take to undergo one complete rotation?

3) What will its angular velocity be after one complete rotation?

4) Provide the magnitude and direction of a force that can be applied at half the radius of the pulley that would establish mechanical equilibrium.

Homework Equations

I=mr^2

The Attempt at a Solution

I'm not asking you to solve it for me, just please help guide me. I have no idea where to begin!

 

[grzz]

What magnitudes are these two forces?

 

[cloudboy]

I'm sorry, here is a picture

So F_2 = 1N and F_1 = 2N
and r = .10m

 

[grzz]

re (1):

For linear motion we use F = Ma.
What formula do we use for rotational motion?

 

[cloudboy]

torque = moment of inertia * angular acceleration

so, since net force = 1n, torque = r * F, so torque = .1N*m.

Angular acceleration = t / I = .667 ms/^2

is that right?

 

[grzz]

Correct.

So find the torque on the pulley.

 

[cloudboy]

Ok I'm trying to figure out the time and I don't really know what to do

 

[grzz]

torque = moment of inertia * angular acceleration

so, since net force = 1n, torque = r * F, so torque = .1N*m.

Angular acceleration = t / I = .667 ms/^2

is that right?

Value of torque is correct. Better use 'T' for 'torque' not to mix it up with the symbol 't' for 'time'!

 

[grzz]

Ok I'm trying to figure out the time and I don't really know what to do

Now to find the time t:

Rotational motion becomes quite simple if one remembers that the equations involved look very much like those used in linear motion.

Up to now we know the initial angular speed \omega_{i}, the angular acceleration \alpha, and the angle turned 2\pi.

Then if we had a problem in linear motion we would know the intial linear speed u, the linear acceleration a and the distance s. To find the time we would use the equation
s = ut + (1/2)at^{2}.

Now let us transer this equation, symbol by symbol from linear motion to rotational motion.

\theta = \omega_{i}t + (1/2)\alphat^{2}.

Put in the values we know and you get the time t.