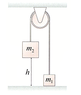
- #1
Jamie_Pi
- 18
- 0
Homework Statement
The two blocks, m1 = 3.3 kg and m2 = 4.8, in the figure below are connected by a massless rope that passes over a pulley. The pulley is 12 cm in diameter and has a mass of 2.0 kg. As the pulley turns, friction at the axle exerts a torque of magnitude 0.64 N · m. If the blocks are released from rest, how long does it take the 4.8 kg block to reach the floor from a height of h = 1.0 m? (Note: If your random numbers do not create movement between the masses enter 0 for your answer.)
Homework Equations
Torque=Force*Radius
Torque=moment of inertia*angular acceleration
angular acceleration = linear acceleration/radius
s=1/2*linear acceleration*time^2
The Attempt at a Solution
I tried to calculate the torque on the pulley and convert that to linear acceleration, and find the time from that.
Torque total= m*g*r-friction
Torque total=4.8*9.8*0.06-4.8*9.8*0.06-0.64
Torque total=0.4004
moment of inertia=1/2*mass*radius^2
moment of inertia=0.0036
0.4004=0.0036*angular acceleration
angular acceleration=111.22
111.22=linear acceleration/0.06
linear acceleration=6.6733
s=3.337*t^2
1=3.337*t^2
t=sqrt(1/3.337)
t=0.5441
I did something wrong, and I'm not sure what. I'm not very good with rotation and torque, though, so I don't know where my mistake could be. The real answer is 2.12 seconds.