dumbdumNotSmart
- 41
- 3
I'm having a hard time undertanding a concept of moment of inertia and Angular acceleration.
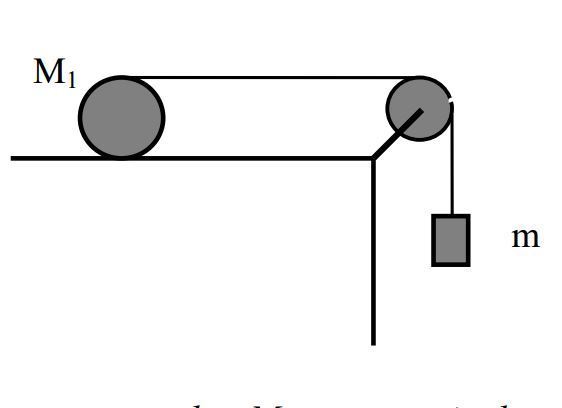
We have a closed system above. M1 is a cylinder of 2 Kilograms, moment of inertia of a cylinder ( MR2 /2 ) with a string tightly rolled around it. This string connects to a free hanging mass (m kilograms) from a ideal massless pulley like in the picture. Gravity is present but has uknown value. The surface under M1 has a static friction coefficient of .1 . When the System is released from Rest the mass descends. The Radius of the cylinder (R) is unknown.
Determine the maximum value of m so that the cylinder rolls without sliding
Sum of Moment of inertias on Cylinder = MR2 /2 . α
α.R=a
F=ma
μE =.1
let a be acceleration of the string (mass m) and acm be the acceleration of M's center of mass. Ψ will be the force of friction.
mg-T=ma
m= T/(g-a)
T+Ψ=Macm (Ψ and T vectors have same direction.
My problem with this case stems from the moment of inertia equation.
We have the following:
TR -ΨR=(MR2 /2)α
Simplifying we get 2T -2Ψ=MRα
In the solution given to us by the teacher, multiplying the angular acceleration by the radius would give us the acceleration of the center of mass of the cylinder. I feel something is wrong since usually the equation gives the acceleration for the edge of the cylinder which is not the same as the center.
Homework Statement
We have a closed system above. M1 is a cylinder of 2 Kilograms, moment of inertia of a cylinder ( MR2 /2 ) with a string tightly rolled around it. This string connects to a free hanging mass (m kilograms) from a ideal massless pulley like in the picture. Gravity is present but has uknown value. The surface under M1 has a static friction coefficient of .1 . When the System is released from Rest the mass descends. The Radius of the cylinder (R) is unknown.
Determine the maximum value of m so that the cylinder rolls without sliding
Homework Equations
Sum of Moment of inertias on Cylinder = MR2 /2 . α
α.R=a
F=ma
μE =.1
The Attempt at a Solution
let a be acceleration of the string (mass m) and acm be the acceleration of M's center of mass. Ψ will be the force of friction.
mg-T=ma
m= T/(g-a)
T+Ψ=Macm (Ψ and T vectors have same direction.
My problem with this case stems from the moment of inertia equation.
We have the following:
TR -ΨR=(MR2 /2)α
Simplifying we get 2T -2Ψ=MRα
In the solution given to us by the teacher, multiplying the angular acceleration by the radius would give us the acceleration of the center of mass of the cylinder. I feel something is wrong since usually the equation gives the acceleration for the edge of the cylinder which is not the same as the center.