cheinbokel
- 1
- 0
I think I've gotten it but figured it would be best to get a second opinion because I feel like I made a few leaps of faith. I sincerely appreciate your time. <3
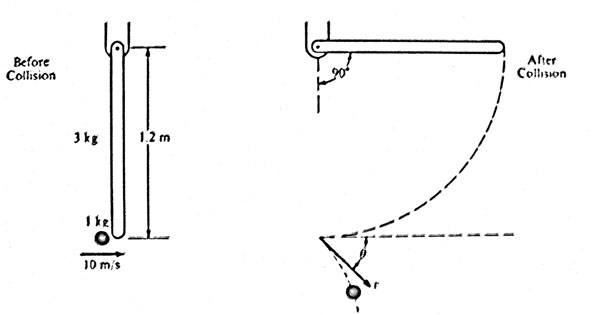
A 1.0 kilogram object is moving horizontally with a velocity of 10m/s, when it makes a collision with the lower end of a bar that is hanging vertically at rest. For the system of the bar and object, linear momentum is not conserved but kinetic energy is. The bar, of length l = 1.2m and mass m = 3kg, is pivoted about its upper end. Immediately after the collision, the object moves with speed v at an angle (theta) relative to its original direction. The bar swings freely, reaching a maximum angle of 90 degrees with respect to the vertical. The moment of inertia for the bar about the pivot is I = (ml^2) / 3. Ignore all friction.
Synopsis:
1.0kg object moving horizontally at 10m/s.
1.2m, 3kg bar I = (ml^2) / 3 suspended about its upper end.
Object hits the bottom of the bar in a glancing collision.
Bar then pivots up to 90 degrees with respect to the vertical.
Object then deflects to an angle \theta below the horizontal at a velocity v.
Diagram:
Questions:
The all-important: F = ma
Conservation of angular momentum: L_i = L_f
Conservation of kinetic energy: K_o = K_ol + K_b
Angular momentum around a point: L = mvr sin(\theta)
\tau = F(lever arm) = I\alpha
L = I\omega
Enclosed in quotes to make it easier to see.
Thanks so much!
Homework Statement
A 1.0 kilogram object is moving horizontally with a velocity of 10m/s, when it makes a collision with the lower end of a bar that is hanging vertically at rest. For the system of the bar and object, linear momentum is not conserved but kinetic energy is. The bar, of length l = 1.2m and mass m = 3kg, is pivoted about its upper end. Immediately after the collision, the object moves with speed v at an angle (theta) relative to its original direction. The bar swings freely, reaching a maximum angle of 90 degrees with respect to the vertical. The moment of inertia for the bar about the pivot is I = (ml^2) / 3. Ignore all friction.
Synopsis:
1.0kg object moving horizontally at 10m/s.
1.2m, 3kg bar I = (ml^2) / 3 suspended about its upper end.
Object hits the bottom of the bar in a glancing collision.
Bar then pivots up to 90 degrees with respect to the vertical.
Object then deflects to an angle \theta below the horizontal at a velocity v.
Diagram:
Questions:
1. Determine the angular velocity of the bar immediately after the collision
2. Determine the speed v of the 1-kilogram object immediately after the collision
3. Determine the magnitude of the angular momentum of the object about the pivot just before the collision
4. Determine the angle \theta.
Homework Equations
The all-important: F = ma
Conservation of angular momentum: L_i = L_f
Conservation of kinetic energy: K_o = K_ol + K_b
Angular momentum around a point: L = mvr sin(\theta)
\tau = F(lever arm) = I\alpha
L = I\omega
The Attempt at a Solution
Enclosed in quotes to make it easier to see.
1. Determine the angular velocity of the bar immediately after the collision
K_t + K_r = K_f + U_f -- K_t and K_f are both zero
K_r = U_f
(1/2)I\omega^2 = mgh
(1/2)[(ml^2)/3]\omega^2 = 3kg * 10m/s * 1.2m/2 -- On the right is a leap of faith. I'm pretty sure the center of mass is what I need to account for here, and that's only moving 0.6m, so I used that.
[3kg * (1.2m)^2 / 6]\omega^2 = 18J
0.72\omega^2 = 18J
\omega = 5rad/s
2. Determine the speed v of the 1-kilogram object immediately after the collision
Total kinetic energy is conserved.
Subscript o represents object, b represents bar.
K_i = K_f -- Initial kinetic energy equals final kinetic energy.
(1/2)mv^2_o = (1/2)mv^2_o + (1/2)I\omega^2
(1/2) * 1kg * (10m/s)^2 = (1/2) * 1kg * V^2_f + (1/2)[(1/3)ml^2]\omega^2
50J = (1/2)V^2_f + (1/6) ml^2\omega^2
50J - [(1/6)3kg * (1.2m)^2] * [5rad/s]^2 = (1/2)V^2_f
32m^2/s^2 = (1/2)v^2_f
v_f = 8m/s
3. Determine the magnitude of the angular momentum of the object about the pivot just before the collision
L = mvr sin(\theta)
L = 1kg * 10m/s * 1.2m * 1
L_i = 12kg m^2/s
4. Determine the angle \theta.
L = mvr sin(\theta)
L = 1kg * 8m/s * 1.2m * sin(\theta)
L = 9.6sin(\theta)
L_b = I\omega
L_b = [(ml^2)/3] * 5rad/s
L_b = 7.2kg m^2/s
12kg m^2/s - 7.2kg m^2/s = 4.8kg m^2/s -- Plug this into the equation above...
4.8kg m^2/s = 9.6kg m^2/s sin(\theta)
sin(\theta) = 0.5
\theta = 30 degrees
Thanks so much!
Last edited: