You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is Angular velocity: Definition and 863 Discussions
In physics, angular velocity or rotational velocity (
ω
{\displaystyle {\boldsymbol {\omega }}}
or
Ω
{\displaystyle {\boldsymbol {\Omega }}}
), also known as angular frequency vector, is a vector measure of rotation rate, that refers to how fast an object rotates or revolves relative to another point, i.e. how fast the angular position or orientation of an object changes with time.
There are two types of angular velocity. Orbital angular velocity refers to how fast a point object revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin. Spin angular velocity refers to how fast a rigid body rotates with respect to its center of rotation and is independent of the choice of origin, in contrast to orbital angular velocity.
In general, angular velocity has dimension of angle per unit time (angle replacing distance from linear velocity with time in common). The SI unit of angular velocity is radians per second, with the radian being a dimensionless quantity, thus the SI units of angular velocity may be listed as s−1. Angular velocity is usually represented by the symbol omega (ω, sometimes Ω). By convention, positive angular velocity indicates counter-clockwise rotation, while negative is clockwise.
For example, a geostationary satellite completes one orbit per day above the equator, or 360 degrees per 24 hours, and has angular velocity ω = (360°)/(24 h) = 15°/h, or (2π rad)/(24 h) ≈ 0.26 rad/h. If angle is measured in radians, the linear velocity is the radius times the angular velocity,
v
=
r
ω
{\displaystyle v=r\omega }
. With orbital radius 42,000 km from the earth's center, the satellite's speed through space is thus v = 42,000 km × 0.26/h ≈ 11,000 km/h. The angular velocity is positive since the satellite travels eastward with the Earth's rotation (counter-clockwise from above the north pole.)
Angular velocity is a pseudovector, with its magnitude measuring the angular speed, the rate at which an object rotates or revolves, and its direction pointing perpendicular to the instantaneous plane of rotation or angular displacement. The orientation of angular velocity is conventionally specified by the right-hand rule.
View More On Wikipedia.org
ω
{\displaystyle {\boldsymbol {\omega }}}
or
Ω
{\displaystyle {\boldsymbol {\Omega }}}
), also known as angular frequency vector, is a vector measure of rotation rate, that refers to how fast an object rotates or revolves relative to another point, i.e. how fast the angular position or orientation of an object changes with time.
There are two types of angular velocity. Orbital angular velocity refers to how fast a point object revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin. Spin angular velocity refers to how fast a rigid body rotates with respect to its center of rotation and is independent of the choice of origin, in contrast to orbital angular velocity.
In general, angular velocity has dimension of angle per unit time (angle replacing distance from linear velocity with time in common). The SI unit of angular velocity is radians per second, with the radian being a dimensionless quantity, thus the SI units of angular velocity may be listed as s−1. Angular velocity is usually represented by the symbol omega (ω, sometimes Ω). By convention, positive angular velocity indicates counter-clockwise rotation, while negative is clockwise.
For example, a geostationary satellite completes one orbit per day above the equator, or 360 degrees per 24 hours, and has angular velocity ω = (360°)/(24 h) = 15°/h, or (2π rad)/(24 h) ≈ 0.26 rad/h. If angle is measured in radians, the linear velocity is the radius times the angular velocity,
v
=
r
ω
{\displaystyle v=r\omega }
. With orbital radius 42,000 km from the earth's center, the satellite's speed through space is thus v = 42,000 km × 0.26/h ≈ 11,000 km/h. The angular velocity is positive since the satellite travels eastward with the Earth's rotation (counter-clockwise from above the north pole.)
Angular velocity is a pseudovector, with its magnitude measuring the angular speed, the rate at which an object rotates or revolves, and its direction pointing perpendicular to the instantaneous plane of rotation or angular displacement. The orientation of angular velocity is conventionally specified by the right-hand rule.
View More On Wikipedia.org
-
A
Comparison between two Tippe tops
I think that the second tippe top will spin on its stem first, and the first tippe top will stop spinning first due to its greater mass and lower angular velocity. Here are my ideas: They are given the same initial energy. By the conservation of energy principle, an object with greater mass...- abrahamabraham
- Thread
-
- Tags
- Angular velocity Energy
- Replies: 1
- Forum: Introductory Physics Homework Help
-
D
Rotation matrix of three intrinsic rotations
I have three frames. The first is the fixed global frame. the second rotates an angle PHIZ with respect to the first. And the third first rotates a PHIX angle with respect to the x axis of the second frame, and then rotates a PHIY angle with respect to the last y axis. That is, there are a total...- dbeckam
- Thread
- Replies: 3
- Forum: Mechanical Engineering
-
I
Investigation regarding the rotor ride
So far some of the topics I can think of are Investigating how angular velocity affects the centripetal force experienced by riders on the rotor or the coefficient of friction required to pin the rider to the wall.- Inaaya
- Thread
- Replies: 8
- Forum: Introductory Physics Homework Help
-
J
I Speed of Light Could be Reached and Indeed even Exceeded
If I mount a fast spinning motor - let's say a 250k rpm, inside a cylinder, and use this cylinder as the armature of the second cylinder that sits round the first one and has the same rpm with the angular velocity in the same direction as the first one, and continue building these layers of fast...- James1355
- Thread
- Replies: 21
- Forum: Special and General Relativity
-

Brownian Ratchet (exercise framed by Feynman's Lectures, l. 46)
1. (d) Both clockwise and counterclockwise rotation, with no net direction. Because the pawl, which is also at the same temperature as the paddle and the ratchet, will undergo Brownian motion and bounce up and down randomly. Sometimes, it will fail to catch the ratchet teeth and allow the...- Hak
- Thread
-
- Tags
- Angular velocity
- Replies: 32
- Forum: Introductory Physics Homework Help
-

Angular Velocity of a Large Pendulum on Earth as seen from the stars
I don't understand the question. how am I supposed to find the magnitudes and directions of the velocity from the figure?- Asem
- Thread
- Replies: 11
- Forum: Introductory Physics Homework Help
-

I Angular velocity of a rod and what formula to use while solving.
The question is: A uniform rod of length ##L## stands vertically upright on a smooth floor in a position of unstable equilibrium. The rod is then given a small displacement at the top and tips over. What is the rod's angular velocity when it makes an angle of 30 degrees with the floor, assuming...- brochesspro
- Thread
- Replies: 15
- Forum: Mechanics
-
A
Question involving clockwise angular movement
v=1.00*8=>v=8 rad/s ar=>100*8^2=>ar=64 rad/s^2 at=1.00*4=>at=4 rad/s^2 The only question I have is ar=-64 rad/s^2, not 64 rad/s^2 as I calculated. I believe this is because the wheel is accelerating in a clockwise direction. However this is not indicated by the mathematical equation. How do I...- as2528
- Thread
- Replies: 9
- Forum: Introductory Physics Homework Help
-
A
Question involving angular acceleration of a spinning wheel
wfinal=98.0 rad/s, dt=3.00s w=(37 revs/3)=>w=(37 revs*(2*pi/1))/3=>w=77.493 a=(98-77.493)/3=>a=6.8357 My answer is exactly half of the correct answer. Where did I go wrong?- as2528
- Thread
- Replies: 12
- Forum: Introductory Physics Homework Help
-

Change in Angular Velocity While Orbiting With No Torque
The planet is faster when it is closer to the planet because when it is closer to the planet it has less rotational inertia, and rotational momentum is conserved in this system, so less rotational inertia means a greater angular velocity. This explains why it is slower when it is farther away...- uSee2
- Thread
- Replies: 30
- Forum: Introductory Physics Homework Help
-
Z
Angular velocity of an airplane
Speed = 900km/hour tan(α)=900t/10000 α=arctan(900t/10000) Derivative is 900/(10000+81 t^2)- Zoubayr
- Thread
- Replies: 18
- Forum: Introductory Physics Homework Help
-
D
I Can a Satellite Maintain its Angular Velocity with Continuous Low Thrust?
Suppose two satellites are in a circular heliocentric orbit with radius R and with angular velocity O'. Satellite 2 then undergoes a low continuous thrust. Can Satellite 2 (the one that undergoes the continuous low thrust) maintain the same angular velocity O' about the sun? It seems that...- dansmith170
- Thread
- Replies: 2
- Forum: Astronomy and Astrophysics
-
A
Angular Velocity from KE, radius, and mass
I tried using the equation w^2 = (4*K)/(mr^2) but I don't think this is right... I got my answer to be 3.2243 and that's not correct- aivilo775
- Thread
- Replies: 4
- Forum: Introductory Physics Homework Help
-
R
I Changes to a spinning skater's angular velocity
Can we describe what is happening as the skater's angular velocity increases/decreases using F=ma rather than invoking L = constant?- Rosenthal
- Thread
- Replies: 4
- Forum: Classical Physics
-

Angular Velocity in the Rotating systems
Summary: Consider a body which is rotating with constant angular velocity ω about some axis passing through the origin. Assume the origin is fixed, and that we are sitting in a fixed coordinate system ##O_{xyz}## If ##\rho## is a vector of constant magnitude and constant direction in the...- WMDhamnekar
- Thread
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Calculating final rotational speed from angular velocity
I have no idea how to go about this. Any help would be appreciated thanks :) Edit: I converted the 1.5 rev/s to rad/s = 9.4 rad/s- Anmol Dubey
- Thread
- Replies: 6
- Forum: Introductory Physics Homework Help
-
D
I Solving for Angular Velocity After a Disc Collision
Hello to everyone, first of all shame on me I has to ask and can not figure out it by myself... The problem is I am trying to code game where two homogenous discs with same mass and same diameter, no fricition due to gravitational forces, can collide. I can figure out the speed and direction...- daavid
- Thread
- Replies: 13
- Forum: Classical Physics
-

I Angular Velocity: Vector or Not?
I understand that angular velocity is technically not a vector so does that mean the cross product of the radius vector and the angular velocity vector, the tangential vector, is also not a vector?- e2m2a
- Thread
- Replies: 5
- Forum: Classical Physics
-
D
Angular velocity of pinned rod
My line of thinking is as follows: \omega_{PQ} = \frac{v_{\perp}}{\ell} = \frac v\ell \frac{\sqrt3}{2} Similarly for rod ##QR## \omega_{QR} = \frac{v_{\perp}}{\ell} = \frac v\ell \frac{\sqrt3}{2} Is my reasoning correct?- DrNG
- Thread
- Replies: 5
- Forum: Introductory Physics Homework Help
-
L
Calculate the angular velocity for each case
First case, descends with the wheel: mgh = .5(I)(w^2) ———- GPE converted to wheel energy w = .1095. ———- rotation result is .1095 Second case, allow to free fall and impulse: mgh = .5(m)(v^2). ———- GPE converted to kinetic energy v = 7.746 ———-...- leafy
- Thread
- Replies: 5
- Forum: Introductory Physics Homework Help
-
P
Angular velocity of rod and bug
I(i)w(i)= I(f)w(f) I(i)= 1.08 x 10-3 kg·m2 w(i)= 0.221 rad/s I(f)= mr^2 + I(i) = (5 x 10^-3)(.138)^2 + (1.08 x 10^-3) (1.08 x 10-3)(.221) = ((1.08 x 10^-3)+9.22 x 10^-5))w(f) w(f) = (2.3868 x 10^-4)/(0.00117522) w(f)= 0.203094 rad/s This is my attempt; however, I cannot seem to get it...- p37
- Thread
- Replies: 6
- Forum: Introductory Physics Homework Help
-
T
Angular Velocity: Pulley and belt system
So far I have: The velocity of the belt will be the same for pully A and D, so we can calculate the angular velocity of pulley D: ## V_A = V_B ## ## \omega_A r_A = \omega_D r_D ## ## ((20*3)+40)(0.075) = \omega_D (0.025) ## ## \omega_D = 300 Rad/s ## My next step was to determine the angular...- thatstheguy9
- Thread
- Replies: 11
- Forum: Introductory Physics Homework Help
-
N
Engineering Find the velocity and angular velocity of the rod and point
Hi everyone :)! I resolve this problem with components method and trigonometry method. My results with components method its okay, but i can´t obtain the correct VE velocity. Im sure that the problem its in the angles, but i don't know how to fix it. The correct answers: -Angular velocity...- Noob of the Maths
- Thread
- Replies: 10
- Forum: Engineering and Comp Sci Homework Help
-
N
Find the angular velocity of this linkage
Hi! everyone! ;) I have a problem with the development of this problem. I need to resolve it with 2 procedures: trigonometry and instant centers. My advance can be see in the next image: The instant centers procediment its (1) up and trigonometry procediment its (2) down. I know that the...- Noob of the Maths
- Thread
- Replies: 8
- Forum: Precalculus Mathematics Homework Help
-
I Apparent angular velocity (inclined orbit)?
Here's the problem setup, my student and I are stuck. A disk is rotating at constant angular velocity ω, and we are watching a point on the rim, parameterized by the angular position θ, move. Because we are observing the motion from an inclination angle Ψ, we do not always observe the...- Andy Resnick
- Thread
- Replies: 11
- Forum: General Math
-
B
Existential dilemma on angular velocity of a complex rigid body
I assumed the angular velocity of the center of mass of the two discs about z axis to be w1 note that angular velocity of center of mass of both discs and center of anyone disc about z axis is same, you can verify that if you want, me after verifying it will use it to decrease the length of the...- bhupesh
- Thread
- Replies: 25
- Forum: Introductory Physics Homework Help
-
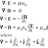
Measure angular velocity and acceleration from missing tooth wheel
Hi, I need to come up with a math model for a digital ignition system. I've been thinking about it and I think that I need to measure 2 things to be able to calculate when I have to start charging the coil. They are the angular velocity and the acceleration but how can I do it? the idea is to... -

Terminal angular velocity of Disc in magnetic field
Torque appiled by smaller disc = mga emf of disc due to B = Bwr2/2 Current I = Bwr2/2R force = IBr = Bwr3/2r torque = rF = Bwr4/2r mga = Bwr4/2r- Advay
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-
V
How to determine angular velocity about a certain axis?
If the crawling insect were stationary at a certain instant of time, then it would have the same angular velocity as that of disk, which is w in a clockwise direction. But now it's velocity at any instant is the vector sum of velocity due to rotation and the velocity it crawls at. My attempt is...- vcsharp2003
- Thread
- Replies: 10
- Forum: Introductory Physics Homework Help
-

Finding Angular Velocity in Rotational Motion Problems
53 rpm equals 5.55 rad/sec multiply 5.55 by 2pi to get angular velocity of 34.8717 Is the answer 34.8717? What should I have done to more accurately solve the problem with a better understanding? What other steps should I take when solving similar problems? and lastly, Is the mass relevant...- momoneedsphysicshelp
- Thread
- Replies: 5
- Forum: Introductory Physics Homework Help
-

Engineering Solving for Angular Velocity at Point A - Confused!
So for this question I got the right angular velocity. But I don’t get the same velocity for point A. I don’t understand why it’s cos30, problem asked for V_a when theta = 45 so I used cos45. I have my work below.- Pipsqueakalchemist
- Thread
- Replies: 1
- Forum: Engineering and Comp Sci Homework Help
-

Direction of Angular velocity and Angular momentum?
I am very confused when textbooks say the direction of Angular velocity is perpendicular ot radius and theta for that matter direction is in perpendicular direction. I know this comes from cross product rule but what is the meaning of Angular velocity and Angular momentum directing in upward...- akashpandey
- Thread
- Replies: 9
- Forum: Mechanics
-

I What is the angular velocity of a satellite?
Angular velocity ω is by definition the runned angle dθ per time dt elapsed: ω=dθ/dt. If the time elapsed in the center of the Earth is dt, the dilated time elapsed on satellite is dt′. What is the satellite's angular velocity? Is it dθ/dt or dθ/dt′?- binis
- Thread
- Replies: 132
- Forum: Special and General Relativity
-
H
What is the final angular velocity of the system after the collision?
I calculated as attached and got it right. However, I just wonder why we can't use conservation of energy as the question has already specified 'frictionless', meaning no energy loss and energy distributed to the rotation only.- hidemi
- Thread
- Replies: 4
- Forum: Introductory Physics Homework Help
-

Angular velocity of a weighted rod left free to rotate around a pivot
Hi guys, I don't really know how to solve this problem. The point is finding ##\omega## when ##m_2## passes from ##m_1##'s original position. Ideally, I'm thinking about some conservation of energy/momentum to apply here, but I'm quite confused. Any hint?- greg_rack
- Thread
- Replies: 6
- Forum: Introductory Physics Homework Help
-

Getting the angular velocity using the angular acceleration graph
The answer here is A What i did is getting the area as follows, 2×4×1/2 +3×-6×1/2 +4×-6 = -29 and then use this Δω=ωf-ωi -29=ωf-5 ωf=24 but there is no such choice.- dahoom102
- Thread
- Replies: 3
- Forum: Introductory Physics Homework Help
-
A
Engineering How to find the angular velocity of a rotating drum?
Good day here is the exerciceThe only velocity I do have is the velocity v os the center of pulley 5, I tried to find the center of instantaneous velocity to find the angular velocity of pulley 5 but I couldn't, any hint would be highly appreciated! Best regards!- Amaelle
- Thread
- Replies: 7
- Forum: Engineering and Comp Sci Homework Help
-

Sum of oscillating frequency and angular velocity
The "egg" initially spun around axis 1 with at ##\omega_s##. After being disturbed, it has started to possesses angular velocities along 2 and 3. The question is to find the rotational speed of ##\vec \omega=\vec\omega_1+\vec\omega_2+\vec\omega_3## to a fixed observer. It is calculated that...- Leo Liu
- Thread
- Replies: 11
- Forum: Introductory Physics Homework Help
-
M
Help with Angular Velocity True-False Question
1)Starting at rest, he brings the weights into his chest. His angular velocity increases. 2)A friend throws a third weight so that the student catches it in one of his outstretched hands. No matter what the direction of the throw, the student's angular velocity decreases. 3) Starting with...- MattAstros
- Thread
- Replies: 12
- Forum: Introductory Physics Homework Help
-
A
Angular velocity and angular acceleration of a turbine
Okay so what I've done; I've put the diammter d = 1m as r = 1m The time interval of 4s is t = 4s and the angular velocitys as; ω1 = 20 rad/s ω2 = 40 rad/s Now to get the accelaration. Angular acceleration can be split into two parts tangetial acceleration and radial acceleration What I...- arhzz
- Thread
- Replies: 17
- Forum: Introductory Physics Homework Help
-
A
Angular velocity in terms of Euler angles
In Chapter 4, derivation 15 of Goldstein reads: "Show that the components of the angular velocity along the space set of axes are given in terms of the Euler angles by $$\omega_x = \dot{\theta} \cos \phi + \dot{\psi} \sin \theta \sin \phi, \omega_y = \dot{\theta} \sin \phi - \dot{\psi} \sin... -
E
Orbital and spin angular velocity?
The Wikipedia page for angular velocity makes a big fuss over "spin" and "orbital" angular velocities, but I have checked through Gregory and Morin's textbooks on classical mechanics and haven't found any reference to them at all. They just work with a single quantity, the angular velocity... -
G
What is a "Torsional Constant"?
The question was: I will also include the solution: So, what is the justification of the first formula [ω=√(C/I)]? I know how to derive simple harmonic equations, this one as I guess is probably similar? But I cannot connect as to how C is used exactly. And the second formula [ω'=ωβ], I...- Gourab_chill
- Thread
- Replies: 11
- Forum: Introductory Physics Homework Help
-

Require help with angular velocity and people flying off the planet
My solutions (attempts) : a> w=v/r | r=6.35x10^6m | therefore V=7.04x10^-5 m/s b> speed of rotation is faster at the equator than the pole as w=v/r. As w remains constant, as r increases towards the pole V has to decrease. c> F = W - R d> Stuck here. I presume that I have to use the equation...- RemotePhysics
- Thread
- Replies: 26
- Forum: Introductory Physics Homework Help
-

How Does Resolving Angular Velocity into Components Affect Its Magnitude?
Angular velocity is the degrees by which something rotates over a time period. If I have an angular velocity in one direction and I resolve it into its components, its components would obviously be of lesser value. Here's what I don't get. When I imagine this scenario, I see that the thing...- aspodkfpo
- Thread
- Replies: 27
- Forum: Introductory Physics Homework Help
-
G
Mechanics: Angular Velocity Vector Questions
Answers are the following : (i) v=(2cost)i - (2sint)j -(1/2)k (ii)2.06m/s (iii)2m/s^2 horizontally towards the vertical axis, making an angle of pi/4 with both the I and j axes.- girlwhoneedsmathhelp
- Thread
- Replies: 6
- Forum: Introductory Physics Homework Help
-

Vector potential ##\vec A## in terms of magnetic field ##\vec B##
My solution is making an analogy of the ##\text{Relevant equations}## as shown above, starting from the equation ##\vec \omega = \frac{1}{2} \vec \nabla \times \vec v##. We have ##\vec B = \vec \nabla \times \vec A = \frac{1}{2} \vec \nabla \times 2\vec A \Rightarrow 2\vec A = \vec B \times...- brotherbobby
- Thread
- Replies: 26
- Forum: Advanced Physics Homework Help
-

Pulley angular velocity problem
Further given: - every beam is infinite stiff - pulleys are massless - cables don't stretch, no slip, and frictionless. -Every pulley has a diameter D except pulley Q. Pulley Q has diameter 0.5*D So what I don't understand is how to calculate/determine the velocity at R and S. Can someone help...- jeffrey
- Thread
- Replies: 24
- Forum: Introductory Physics Homework Help
-
P
Rotation of two cylinders inclined at an angle
A single pair of points will be in contact between P and Q. The frictional force will try to make the velocity of these points equal. Say the final angular velocity of Q is ωq. The velocity of points in contact can never be equal because of difference in directions of ωq and ωp. If I break...- PhysicsBoi1908
- Thread
- Replies: 4
- Forum: Introductory Physics Homework Help
-
R
Angular Velocity of a Car going around a curve
θ=90°= π /2 so the instantaneous angular velocity dθ/dt= lim∆ t -> 0 (θ(t + ∆ t)-θ(t))/(∆ t) When I calculate it out it is π /2 radians per second. Is this correct?- RobGoodall
- Thread
- Replies: 9
- Forum: Introductory Physics Homework Help