- #1
cheinbokel
- 1
- 0
I think I've gotten it but figured it would be best to get a second opinion because I feel like I made a few leaps of faith. I sincerely appreciate your time. <3
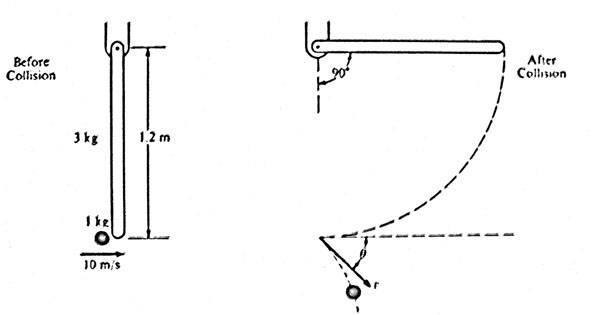
A 1.0 kilogram object is moving horizontally with a velocity of 10m/s, when it makes a collision with the lower end of a bar that is hanging vertically at rest. For the system of the bar and object, linear momentum is not conserved but kinetic energy is. The bar, of length l = 1.2m and mass m = 3kg, is pivoted about its upper end. Immediately after the collision, the object moves with speed v at an angle (theta) relative to its original direction. The bar swings freely, reaching a maximum angle of 90 degrees with respect to the vertical. The moment of inertia for the bar about the pivot is [itex] I = (ml^2) / 3 [/itex]. Ignore all friction.
Synopsis:
1.0kg object moving horizontally at 10m/s.
1.2m, 3kg bar [itex] I = (ml^2) / 3 [/itex] suspended about its upper end.
Object hits the bottom of the bar in a glancing collision.
Bar then pivots up to 90 degrees with respect to the vertical.
Object then deflects to an angle [itex]\theta[/itex] below the horizontal at a velocity v.
Diagram:
Questions:
The all-important: [itex]F = ma [/itex]
Conservation of angular momentum: [itex]L_i = L_f[/itex]
Conservation of kinetic energy: [itex]K_o = K_ol + K_b[/itex]
Angular momentum around a point: [itex]L = mvr sin(\theta)[/itex]
[itex]\tau = F(lever arm) = I\alpha [/itex]
[itex]L = I\omega[/itex]
Enclosed in quotes to make it easier to see.
Thanks so much!
Homework Statement
A 1.0 kilogram object is moving horizontally with a velocity of 10m/s, when it makes a collision with the lower end of a bar that is hanging vertically at rest. For the system of the bar and object, linear momentum is not conserved but kinetic energy is. The bar, of length l = 1.2m and mass m = 3kg, is pivoted about its upper end. Immediately after the collision, the object moves with speed v at an angle (theta) relative to its original direction. The bar swings freely, reaching a maximum angle of 90 degrees with respect to the vertical. The moment of inertia for the bar about the pivot is [itex] I = (ml^2) / 3 [/itex]. Ignore all friction.
Synopsis:
1.0kg object moving horizontally at 10m/s.
1.2m, 3kg bar [itex] I = (ml^2) / 3 [/itex] suspended about its upper end.
Object hits the bottom of the bar in a glancing collision.
Bar then pivots up to 90 degrees with respect to the vertical.
Object then deflects to an angle [itex]\theta[/itex] below the horizontal at a velocity v.
Diagram:
Questions:
1. Determine the angular velocity of the bar immediately after the collision
2. Determine the speed v of the 1-kilogram object immediately after the collision
3. Determine the magnitude of the angular momentum of the object about the pivot just before the collision
4. Determine the angle [itex]\theta[/itex].
Homework Equations
The all-important: [itex]F = ma [/itex]
Conservation of angular momentum: [itex]L_i = L_f[/itex]
Conservation of kinetic energy: [itex]K_o = K_ol + K_b[/itex]
Angular momentum around a point: [itex]L = mvr sin(\theta)[/itex]
[itex]\tau = F(lever arm) = I\alpha [/itex]
[itex]L = I\omega[/itex]
The Attempt at a Solution
Enclosed in quotes to make it easier to see.
1. Determine the angular velocity of the bar immediately after the collision
[tex]K_t + K_r = K_f + U_f [/tex] -- [itex]K_t[/itex] and [itex]K_f[/itex] are both zero
[tex]K_r = U_f[/tex]
[tex](1/2)I\omega^2 = mgh[/tex]
[tex](1/2)[(ml^2)/3]\omega^2 = 3kg * 10m/s * 1.2m/2[/tex] -- On the right is a leap of faith. I'm pretty sure the center of mass is what I need to account for here, and that's only moving 0.6m, so I used that.
[tex][3kg * (1.2m)^2 / 6]\omega^2 = 18J[/tex]
[tex]0.72\omega^2 = 18J[/tex]
[tex]\omega = 5rad/s[/tex]
2. Determine the speed v of the 1-kilogram object immediately after the collision
Total kinetic energy is conserved.
Subscript o represents object, b represents bar.
[tex]K_i = K_f[/tex] -- Initial kinetic energy equals final kinetic energy.
[tex](1/2)mv^2_o = (1/2)mv^2_o + (1/2)I\omega^2[/tex]
[tex](1/2) * 1kg * (10m/s)^2 = (1/2) * 1kg * V^2_f + (1/2)[(1/3)ml^2]\omega^2[/tex]
[tex]50J = (1/2)V^2_f + (1/6) ml^2\omega^2[/tex]
[tex]50J - [(1/6)3kg * (1.2m)^2] * [5rad/s]^2 = (1/2)V^2_f[/tex]
[tex]32m^2/s^2 = (1/2)v^2_f[/tex]
[tex]v_f = 8m/s[/tex]
3. Determine the magnitude of the angular momentum of the object about the pivot just before the collision
[tex]L = mvr sin(\theta)[/tex]
[tex]L = 1kg * 10m/s * 1.2m * 1[/tex]
[tex]L_i = 12kg m^2/s[/tex]
4. Determine the angle [itex]\theta[/itex].
[tex]L = mvr sin(\theta)[/tex]
[tex]L = 1kg * 8m/s * 1.2m * sin(\theta)[/tex]
[tex]L = 9.6sin(\theta)[/tex]
[tex]L_b = I\omega[/tex]
[tex]L_b = [(ml^2)/3] * 5rad/s[/tex]
[tex]L_b = 7.2kg m^2/s[/tex]
[tex]12kg m^2/s - 7.2kg m^2/s = 4.8kg m^2/s[/tex] -- Plug this into the equation above...
[tex]4.8kg m^2/s = 9.6kg m^2/s sin(\theta)[/tex]
[tex]sin(\theta) = 0.5[/tex]
[tex]\theta = 30 degrees[/tex]
Thanks so much!
Last edited: