Angular Speed And Kinetic Energy

[Bashyboy]

The problem I am working on is:

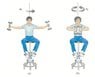
"A student sits on a freely rotating stool holding two dumbbells, each of mass 2.97 kg (see figure below). When his arms are extended horizontally (figure a), the dumbbells are 0.95 m from the axis of rotation and the student rotates with an angular speed of 0.740 rad/s. The moment of inertia of the student plus stool is 2.68 kg · m2 and is assumed to be constant. The student pulls the dumbbells inward horizontally to a position 0.298 m from the rotation axis (figure b).

(a) Find the new angular speed of the student.

b) Find the kinetic energy of the rotating system before and after he pulls the dumbbells inward.
KE before
KE after"

I was able to solve the problem, the calculations being rather simple. My question is, does the act of extending your arms out, whilst grasping the dumbbells in your hand, cause you to have an angular speed? Or do you have to initially have an angular speed to see this changes in the angular speed occur? Also, the final and initial kinetic energy are not equal, why is that? Where did the energy go?

 

[gneill]

I was able to solve the problem, the calculations being rather simple. My question is, does the act of extending your arms out, whilst grasping the dumbbells in your hand, cause you to have an angular speed?

Nope. Consider: if moving the dumbbells straight inwards caused you to spin, how would the Universe decide which way you should rotate? If the initial rotation rate is zero then the angular momentum is zero, too. Angular momentum is conserved, so rotation rate must remain zero.

Or do you have to initially have an angular speed to see this changes in the angular speed occur?

Yup. Think of the rotation rate change as being due to the interaction of the two variables comprising the angular momentum: L = I*ω. If L is conserved then if I goes up, ω must go down accordingly, and vice versa. If L is zero, then no matter what you do with I (except magically disappearing the mass somehow) ω must remain zero.

Also, the final and initial kinetic energy are not equal, why is that? Where did the energy go?

What source or sink for energy does the system have?

 

[Bashyboy]

What source or sink for energy does the system have?

The kinetic energy increases. I figured it would stay the same; since, like you said, angular momentum is conserved, meaning an increase in one variable results in a decrease in the other variable. Kinetic energy due to rotational motion depends on the same variables as angular momentum, so I figured we would see the same behavior.

"Nope. Consider: if moving the dumbbells straight inwards caused you to spin, how would the Universe decide which way you should rotate? If the initial rotation rate is zero then the angular momentum is zero, too. Angular momentum is conserved, so rotation rate must remain zero."

What you said has left me intrigued: what do you mean by "how would the Universe decide which way you should rotate?"

 

[gneill]

The kinetic energy increases. I figured it would stay the same; since, like you said, angular momentum is conserved, meaning an increase in one variable results in a decrease in the other variable. Kinetic energy due to rotational motion depends on the same variables as angular momentum, so I figured we would see the same behavior.

Kinetic energy is not the same as momentum. While momentum is always conserved in a closed system (where there are no external forces acting), kinetic energy is not always conserved (Remember the difference between elastic and inelastic collisions?); there are other places it can go (heat, for example). And kinetic energy can be transformed from other energy sources within the system (chemical, electrical, etc.) . What's the source of the increase in KE that you noticed in this problem?

"Nope. Consider: if moving the dumbbells straight inwards caused you to spin, how would the Universe decide which way you should rotate? If the initial rotation rate is zero then the angular momentum is zero, too. Angular momentum is conserved, so rotation rate must remain zero."

What you said has left me intrigued: what do you mean by "how would the Universe decide which way you should rotate?"

Well, if moving the dumbbells inwards created rotation (and thus angular momentum!) where there was none before, which direction would that rotation take? "Who" or what would decide? What happens to the law of conservation of momentum if it were so?

 

[Bashyboy]

Oh, the system consists of the person; so, the loss in energy would be due to the person.

 

[gneill]

Oh, the system consists of the person; so, the loss in energy would be due to the person.

Loss or gain, depending upon the work he does moving the dumbbells.

 

[Bashyboy]

Yeah, it's a gain in energy, which seems kind of strange.

 

[gneill]

Yeah, it's a gain in energy, which seems kind of strange.

Ask yourself if the dumbbells can be moved "for free", or if work is done.

 

[Bashyboy]

But doesn't the system consist of the person, dumbbells, and stool?

 

[gneill]

But doesn't the system consist of the person, dumbbells, and stool?

Yes...

 

[Bashyboy]

So would the energy just be moving around in the system, then? And the energy would then be conserved?

 

[gneill]

So would the energy just be moving around in the system, then? And the energy would then be conserved?

Well, in general energy is conserved, but often it ends up in forms that can no longer be useful. Like heat due to friction, or sound, etc. After it ends up there it "disappears" from our KE + PE equations.

In this problem there is a source\sink for energy that add or subtract energy from the mechanical system. Think "metabolism"

 

[Bashyboy]

Oh, so the person has do work on the dumbbells against gravity, and the dumbbells gain that energy?

 

[gneill]

Oh, so the person has do work on the dumbbells against gravity, and the dumbbells gain that energy?

No, not gravity. A centripetal force (supplied by the person) holds the dumbbells in their circular motion. The person works against that force to bring the dumbbells in closer. This adds energy (from the work done) to the system. When the person let's them out again work is done on him, transferring energy from the system to him (Question to ponder: what happens to the energy of the work done on the person?).

 

[Bashyboy]

Are you saying that the person has to work against the own force he provides? Shouldn't it be that he has to do work against the centrifugal force (or inertial force)? I still don't understand how this would give the system more energy, doesn't it exhaust one's energy to move dumbbells around?

 

[gneill]

Are you saying that the person has to work against the own force he provides? Shouldn't it be that he has to do work against the centrifugal force (or inertial force)? I still don't understand how this would give the system more energy, doesn't it exhaust one's energy to move dumbbells around?

The person is providing the required centripetal force. If he wants to move the dumbbells, then that force operates through some distance and thus work is done on the system.

Of course it exhausts one's energy to do work. This is why it is important to make sure to feed your lab assistants on a regular basis, to keep their energy supply up

 

[Bashyboy]

Oh, I see. So, the energy goes into the dumbbells. I think I understand it now. Thank you!

 

[gneill]

Oh, I see. So, the energy goes into the dumbbells. I think I understand it now. Thank you!

Well, the energy goes into the system as a whole; to the dumbbell directly and to the stool via any reaction forces operating on the person (who's sitting on the stool...).