MHB Angular Speed of Smaller Wheel

[mathdad]

Let r = radius

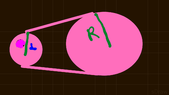
See picture.

If r = 6 cm, R = 10 cm, and the angular speed of the larger wheel is 100 rpm, determine the angular speed of the smaller wheel in radians per minute.

Again, 1 revolution = 2 pi radians.

I need to use w = θ/t.

So, θ = 100 rpm • 2 pi radians.

θ = 200 pi radians

w = 200 pi radians/min, which is my answer.

At this point, I doubted that my answer is right because it did not take long to find w or omega representing the angular speed.

The book's answer is 1000/3 radians/min.

What did I forget to do?

View attachment 7910

 

[skeeter]

f r = 6 cm, R = 10 cm, and the angular speed of the larger wheel is 100 rpm, determine the angular speed of the smaller wheel in radians per minute.

$v = r \omega_1$, where $\omega_1$ is the angular speed of the smaller wheel

$v = R \omega_2$, where $\omega_2$ is the angular speed of the larger wheel.

the belt connecting the two wheels has a fixed linear speed, $v$ ...

$\implies r \omega_1 = R \omega_2$

$\omega_1 = \dfrac{R \omega_2}{r} = \dfrac{10 \cdot 100}{6} = \dfrac{500}{3} \, rpm$

convert $\omega_1$ to radians per minute ...

$\dfrac{500 \, rev}{3 \, min} \cdot \dfrac{2\pi \, rad}{rev} = \dfrac{1000\pi}{3} \, rad/min$

 

[mathdad]

Nicely-done. I will try your solution steps for this question to answer the textbook question where r = 6 cm and R = 10 cm.