Answer: Understanding Multirange Voltmeter Internal Wiring

  • Thread starter Thread starter parm09
  • Start date Start date
  • Tags Tags
    Voltmeter
Click For Summary
The discussion revolves around understanding the internal wiring of a three-scale voltmeter and calculating the resistances R1, R2, and R3 for different voltage ranges (3.00 V, 15.0 V, and 150 V). Participants emphasize the need to apply Ohm's Law (V = I/R) and the relationship between the coil current and resistance (Vcoil = IgRcoil) to solve the problem. The main objective is to determine the overall resistance of the voltmeter for each specified voltage range. Clarification is sought on the exact problem statement to ensure accurate calculations. The conversation highlights the importance of precise problem articulation for effective troubleshooting.
parm09
Messages
4
Reaction score
0
Can someone please help me out with this problem? I am not sure if what I am doing

question:
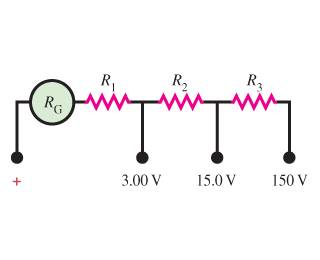
The figure below shows the internal wiring of a "three-scale" voltmeter whose binding posts are marked , 3.00 V, 15.0 V, and 150 V. When the meter is connected to the circuit being measured, one connection is made to the post marked + and the other to the post marked with the desired voltage range. The resistance of the moving coil is Rg, and a current of I in the coil causes it to deflect full scale.

Picutre:
yf_Figure_26_64.jpg


we know v=i/r and Vcoil=IgRcoil

dont know where to begin
 

Attachments

  • yf_Figure_26_64.jpg
    yf_Figure_26_64.jpg
    5.7 KB · Views: 685
Physics news on Phys.org
What is required in the problem?
 
sorry forgot to mention that. you have to find R1, R2, R3. Also find the overall resistance of the meter on a 3.00, 15.0, 150 V-range
 
Why don't you state the entire text of the problem, verbatum? It should have a question mark somewhere to be answered.
 
What is R1, R2, R3 and what is the overall resistance of the meter on a 3.00, 15.0, 150 V-range? that what its asking
 

Thread 'Magnitude of buoyant force in fluids of different densities'

The book claims the answer is that all the magnitudes are the same because "the gravitational force on the penguin is the same". I'm having trouble understanding this. I thought the buoyant force was equal to the weight of the fluid displaced. Weight depends on mass which depends on density. Therefore, due to the differing densities the buoyant force will be different in each case? Is this incorrect?
View full post »

Similar threads

Measurement technology textbook problems
  • · Replies 1 ·
Replies
1
Views
744
Measurement technology textbook problems
  • · Replies 2 ·
Replies
2
Views
652
Potentiometer Problem: 3V Battery, 100cm Sliding Wire, and 60cm Voltmeter
  • · Replies 2 ·
Replies
2
Views
3K
Unraveling the Mystery of EMF Internal Resistance
  • · Replies 2 ·
Replies
2
Views
2K
How Do You Calculate the Series Resistance for a Voltmeter Using a Galvanometer?
  • · Replies 4 ·
Replies
4
Views
2K
Difference in EMF of 5000 V and a voltmeter reading of 40 V
  • · Replies 22 ·
Replies
22
Views
4K
Design a Multirange Voltmeter with Variable Series Resistances
  • · Replies 4 ·
Replies
4
Views
9K
Solve emf of battery with resistors and voltmeter
  • · Replies 4 ·
Replies
4
Views
6K
What is the Voltage read on a Real Voltmeter?
  • · Replies 3 ·
Replies
3
Views
8K
Multirange Ammeter magnitudes homework
  • · Replies 1 ·
Replies
1
Views
3K