karush
Gold Member
MHB
- 3,240
- 5
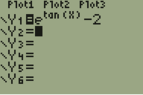
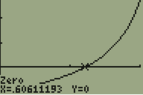
The graph of $y=e^{\tan x} - 2$ crosses the x-axis at one point in the interval [0,1]. What is the slope of the graph at this point.
A. 0.606
B 2
C 2.242
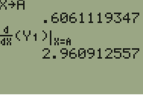
D 2.961
E 3.747ok i tried to do a simple graph of y= with tikx but after an hour trying failed
doing this in demos it seens the answer is D
I know you take the differential set it to zero and that should give you the x value of intersection
A. 0.606
B 2
C 2.242
D 2.961
E 3.747ok i tried to do a simple graph of y= with tikx but after an hour trying failed
doing this in demos it seens the answer is D
I know you take the differential set it to zero and that should give you the x value of intersection