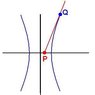
The discussion centers on finding the tangent line to a hyperbola at a specific point. The user seeks assistance in determining the slope of the tangent line that passes through the point P(4/3,0) and touches the hyperbola at point Q(u,v). The relationship between the slope of the tangent line and the derivative dy/dx at point Q is emphasized as crucial for solving the problem. The conversation highlights the importance of understanding derivatives in the context of conic sections.
PREREQUISITESStudents preparing for calculus exams, educators teaching conic sections, and anyone seeking to deepen their understanding of derivatives and tangent lines in relation to hyperbolas.
PrashntS said:
The motive was to find the tangent.. But I can't seem to find it.. when I plot the graph to this yperbola, I just CANT figure out how to proceed! HELP!
PS: This question was in exams today.. If the question is missing some info, please mention -.-
