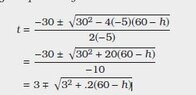Applying quadratic formula to inverse of a function: Calculation problem

[self4u]

Hi - I'm trying to figure out the specific steps in a math textbook. I'm trying to figure out how the textbook did its algebra here with a quadratic formula to find an inverse of a function:

View attachment 5796

Sadly there's a step I'm supposed to know by now in the simplification algebra in there 3 steps shown...and I'm missing it.

From step 2 to step 3...it looks like only part of the equation is divided by the denominator -10. I didn't think it was possible to divide by 10 with individual numbers under the square root symbol. Furthermore - step 3 shows a reduced ".2(60-h)". How did 20 go to .2? How is (60-h) completely unaffected?

Sorry for such a simple question and thank you in advance for your help!

 

[self4u]

Okay I think I've finally figured it out. I'm a dolt. But since I'm a dolt, I might as well post why I'm a dolt due to the order of operations.

Step 2A: Simply divide every single number by -10. So the method to get to Step 3 becomes:

a) (-30/-10) which becomes positive 3.

b) Then (30sq./-10) which becomes -3sq...then becoming 9.

c) Then (20/-10) which becomes -2.

d) Then (60/-10) which becomes -6. At this point we could multiple it with the (-2) above making positive 12.

e) Then (h/-10) which becomes -h/10. At this point we could multiple it with the (-2) above making -2/10h...simplified to -1/5h...or -.2h.

That gets to step 3...remembering to keep the square root above 21 - .2h.

 

[Greg]

$$\begin{align*}\dfrac{-30\pm\sqrt{30^2+20(60-h)}}{-10}&=3\pm\dfrac{\sqrt{30^2+20(60-h)}}{-1\cdot|10|} \\
&=3\pm\dfrac{\sqrt{30^2+20(60-h)}}{-1\sqrt{10^2}} \\
&=3\mp\sqrt{\dfrac{900+20(60-h)}{100}} \\
&=3\mp\sqrt{9+\dfrac15(60-h)}=3\mp\sqrt{3^2+.2(60-h)}\end{align*}$$