Applying the Kutzbach Gruebler criterion to a pantograph

[amrbekhit]

Hello all,

I'm having trouble understanding how to apply the Kutzbach Gruebler equation to all but the simplest of mechanisms.

As I understand it, the DOFs of a mechanism is a sum of the DOFs of all the moving links minus the sum of the all the DOFs constrained by the joints. For a planar four bar linkage with one link grounded, there are 3 moving links (so total DOFs = 3 links * 3 DOF = 9) and 4 rotary joints (constrained DOFs = 4 joints * 2 DOF = 8). The total DOF = 9 - 8 = 1.

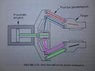
Now consider the pantograph mechanism shown in the attached picture. I can see that there are a total of 7 links (including the base), 6 of which are moving (total DOFs = 6 links * 3 DOF = 18). However, I can only identify 7 joints (5 rotary, 2 prismatic), which would constrain a total of 7 * 2 = 14 DOF, giving the total DOFs as 18 - 14 = 4, which I know is incorrect. According to the book I got the picture out of, there are actually 8 joints, which gives the correct answer of 2 DOF.

Likewise, I also have a problem with the mechanism on the left hand side of the following image:

http://www.cs.cmu.edu/~rapidproto/mechanisms/figures/dcacu.gif

I can see 5 moving links (15 DOF) but only 6 joints (5 rotary and 1 prismatic: 12 DOF) instead of 7, giving a total DOF = 3, whereas the correct answer (according to the site) is 1.

So, for some reason, there always seems to be an extra joint that I'm unable to identify. What am I missing?

Thanks

Amr

 

[timthereaper]

It seems you're forgetting to count the joint multiple times on the mechanism that joins more than 2 links. On the pantograph, you have to count the joint that joins links 2, 4, and 5 twice. On the left hand side of the image you linked to, joint C needs to be counted twice because it joins links 2, 3, and 4. Any time N links are constrained by the same pin joint, you count that joint N-1 times.

 

[amrbekhit]

Ah that's it, thanks. That explains what the book meant when it was describing ternary and quaternary joints.

 

[amrbekhit]

I've attached a photo for another mechanism that is keeping me scratching my head.

As far as I can tell, this is a 1DOF mechanism, with a single linear actuator allowing the fingers to rotate together about a certain point.

I've highlighted in the image where I think the moving links are. I reckon that each pinion and adjoining link are rigidly linked, and connected to ground via a pin joint.

The list of moving links is:

• 1 x Linear actuator/rack (dark green).
• 2 x Pinion/inside link (blue, magenta).
• 2 x Outside link (red, lime).
• 2 x Finger (brown, black).

Resulting in 7 links and a total of 7 * 3 = 21 DOF.

The list of joints is:

• 1 x prismatic joint.
• 2 x rack/pinion joint.
• 8 x revolute joint.

Resulting in 11 joints a total of 11 * 2 = 22 constrained DOF.

Unfortunately, this would imply that the mechanism is overconstrained, which it isn't. What am I missing?

Amr