Approximating smooth curved manifolds with "local bits" of curvature?

[Spinnor]

Consider the electric and magnetic fields around a dipole antenna,

Suppose these fields represent some type of curvature in space and time. Suppose where the fields are strong we have greater curvature. Also suppose these fields are really some very large but finite sum of "moving local bits" of curvature whose sum closely represents the classical fields above. So the question is can we get smooth curved manifolds from small local bits of curvature if we don't look too closely, (any small volume we might look at would contain many bits whose curvature overlaps and averages). Is there a branch of mathematics that might deal with this?

Thanks.

 

[docnet]

Edit:

If I'm understanding right, you can numerically model such a system as a function of space and time by assigning time-dependent vectors to predetermined 3-d grid points. A loose motivation is to evaluate the points as vectors of a vector field on a higher dimensional manifold. The grid spacing can be as fine as you want within reason, but you can't cover with a finite number of points.

Consider the electric and magnetic fields around a dipole antenna,

View attachment 344716

View attachment 344717
Suppose these fields represent some type of curvature in space and time. Suppose where the fields are strong we have greater curvature. Also suppose these fields are really some very large but finite sum of "moving local bits" of curvature whose sum closely represents the classical fields above. So the question is can we get smooth curved manifolds from small local bits of curvature if we don't look too closely, (any small volume we might look at would contain many bits whose curvature overlaps and averages). Is there a branch of mathematics that might deal with this?

Thanks.

If I'm understanding right, you can numerically model such a system as a function of space and time by assigning time-dependent vectors to predetermined 3-d grid points. A loose motivation is to evaluate the points as components of a vector field of higher dimensional manifold. The grid spacing can be as fine as you want within reason, but you can't cover $\mathbb{R}^3$ with a finite number of points.

Explain 'moving local bits'.

 

[docnet]

My reply disappeared because the site is glitchy on my phone. I'll post a mother reply later

 

[Spinnor]

If I'm understanding right, you can numerically model such a system as a function of space and time by assigning time-dependent vectors to predetermined 3-d grid points. A loose motivation is to evaluate the points as components of a vector field of higher dimensional manifold. The grid spacing can be as fine as you want within reason, but you can't cover $\mathbb{R}^3$ with a finite number of points.

Explain 'moving local bits'.

I am having trouble coming up with a clear answer so will have to think a bit more. Thanks.

 

[Spinnor]

Again consider the electric fields surrounding an antenna at an instant of time.

We know that an antenna emits energy, suppose the energy is in the form of a very large but finite number of particles which move away from the antenna at the speed of light. Google "how many photons does a typical radio signal emit" the result begins,

• 1 Watt transmitter at 100 MHz: Emits about 1E25 photons per second, or about 100 billion photons per square meter of reception area per second at a range of 60 miles
• 1 kW radio transmitter at 800 Hz: Emits 1.88 × 10³³ photons per second
• 84-kW AM radio station at 1000 kHz: Emits 1.272 x 10^32 photons per second
• 940 kHz radio station: Emits 4 × 10^31 photons per second
• FM radio station at 98.1 MHz: Emits 7.7 × 10^29 photons per second
  

Suppose that associated with each particle is a wavelength inversely proportional to their energy. We might also associate a helicity with each particle, of either left or right handed type.

Now the problem is, can we associate electric and magnetic fields with each particle such that the square of these fields (which is a measure of energy density) is significant only in a volume of order the wavelength cubed centered on the particle. When there are very many particles emitted per second from the antenna we want the fields of each particle to sum to the classical fields shown above.

The electric and magnetic fields far from the antenna have the property that the divergence of the fields is zero, the field lines form closed loops. Let us assume the fields associated with each particle also have this property that their divergence is zero, local fields of zero divergence sum to global fields of zero divergence (local used in the sense that the energy and thus the fields of a particle is mostly confined to a volume of order the wavelength cubed).

The moving local bits are then the wavelength sized regions of electric and magnetic fields that move at the speed of light.

One might want to consider how fields look in a frame of reference that moves away or towards the antenna with constant velocity. Relativity theory constrains our ideas. For example, relativity tells us that there is a velocity we can move away from the antenna such that particles that move right past us will have their energy halved and their wavelength doubled, red-shift. One might ask if the fields we assigned to each particle in our rest frame transform in the right way according to the special theory of relativity in a moving frame of reference.

To move forward I think one needs to just guess at some approximate set of fields and examine if this approximation makes any sense at all.

Thanks for your suggestions.

 

[Spinnor]

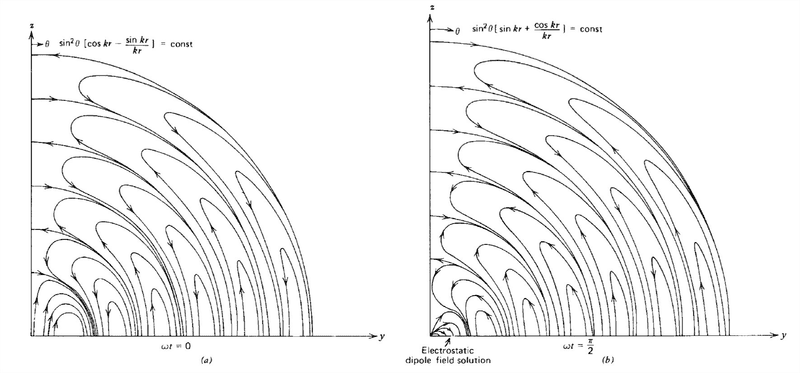
The dipole field pattern below might work as a 2 dimensional "building block" for the fields of our bits. It shows some promise and potential problems.

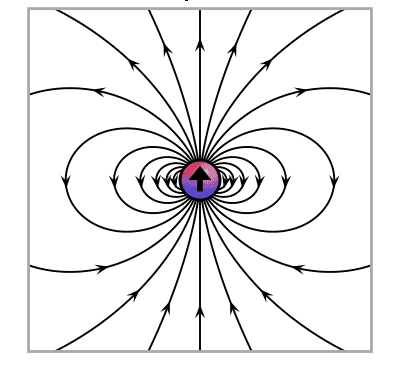
Let the graph above represent the electric field of a point dipole in 2 dimensions (I think the graph is the field of a point dipole in 3 dimensions but the gross properties are the same in 2 dimensions?). One must imagine removing the circle above with the single large arrow and then continuing the field lines towards the center. Let this field pattern be a 2 dimensional slice of the electric field of our bit at some instant in time. Suppose we look towards the antenna our field observation plane above is then perpendicular to the line of sight towards the antenna. As the bit passes through our observation plane let the field pattern above rotate either clockwise or counter clockwise with the frequency of the radiation from the antenna. Let one full rotation of the electric field arbitrarily represent the fields of one bit, the electric field of our bit has one full twist about the propagation direction, our bit is arbitrarily one wavelength long. The arbitrary one twist is a bit ugly but lets start with that.

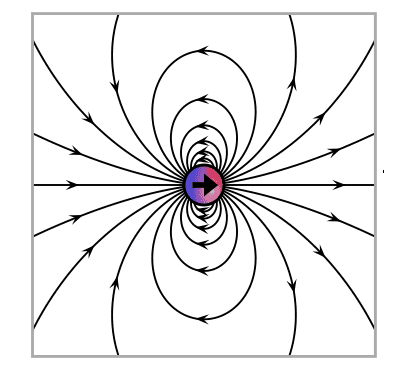
Take the above graph and rotate it 90 degrees to get the magnetic field of our bit (no explanation why for now, it just seems to work), it rotates in the same plane as the electric field, always ahead or behind by 90 degrees. Let it also undergo one full rotation to give the magnetic field of our bit. If we overlay the two graphs I think they have the interesting property (when using the correct 2 dimensional graphs) that where ever the E and B field lines meet they do so at right angles (See the 10:55 minute mark of the video, Fluid Mechanics Lesson 12F: Superposition in Potential Flow, )?

As a check for our toy fields we want the cross product of the electric and magnetic fields, E X B, to be proportional to the energy and momentum flows. My fields above give linear momentum but no angular momentum, show this by evaluating E X B at 4 symmetric points, you get only momentum in the direction of propagation and no angular momentum? We need to tweak the field patterns above to get angular momentum. The field lines must have components in the direction of propagation to get angular momentum? I think this might be approximated by evaluating the electric field of two infinitely long 1 dimensional oppositely charged lines twisted around each other somewhat like a DNA helix (one twist per wavelength) in the limit that distance between the lines goes to zero and charge density goes to infinity keeping the product of the charge density and separation distance a constant. This should give us an electric field with components in the direction of propagation and perpendicular to the propagation direction?

As a check we would like the angular momentum of our bits to be independent of the energy, we want the angular momentum to be quantized, this puts a severe constraint on our guess.

As a check we will want the energy of each bit (E^2 + B^2 integrated over all space) to be finite and to be inversely proportional to the wavelength of the bit, that could be trouble as the fields grow very large near the axis of the bit.

As a check we want the field lines to have zero divergence and I think they do as long as the observation volume contains one bit?

As a check we want the fields of many bits to sum to the classical fields of an antenna. I don't know how to show or argue this.

There is a term in Maxwell's equations called the displacement current. We are told it is not a real current but it still has the dimensions of a "real" current. The displacement current is simply the time rate change of the electric field. Far from the antenna this current has the interesting property that the graph of this current looks exactly like the graph of the electric field but shifted in time by 90 degrees and normalized. The mathematics of Maxwell's equations may allow us to think of our bits as a propagating, localized, mostly transvers flow of some type of current that gives rise to electric and magnetic fields?

Maybe there is a connection between displacement current and some bit of curvature of space that is a function of space and time and can propagate?

Thanks for any thoughts or corrections.