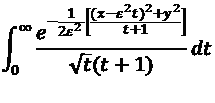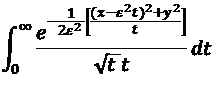I Approximation of a function with another function

[umby]

Hi,
I am wondering if it is possible to demonstrate that:

tends to

in the limit of both x and y going to infinity.

In this case, it is needed to introduce a measure of the error of the approximation, as the integral of the difference between the two functions? Can this be viewed as a norm in some space? Thanks in advance.

 

[andrewkirk]

Maybe I'm missing something ( I've only just woken up!) but it looks to me as though neither integral converges, as there will be some $x'$ such that $\forall x>x'$ both integrands exceed
$$\frac12 t^{-\frac32}\exp\left(\frac{\varepsilon^2t}2 \right)$$
which increases without limit, as the second term dominates the first.

If that's right then there can be no such approximation, as neither integral exists.

 

[umby]

You are full right! It was my fault. Unfortunately, I cannot write formulae correctly in this forum, so I did a picture of my integrals, but the resolution was very bad.
The correct integrals are:

and

.
I lost the minus in the conversion process.
You can interpret x and y as related by the equation $r^2 = x^2+y^2$.
For example, for ε = 0.01 (I am interested in the case where ε > 0), but the same happen for other values of ε, for x and y increasing along the diagonal, i.e. x = y, for x going from 0.005 to 0.6 with pass 0.05, the difference between the two integrals are:
$-0.771824, 0.00263352, 0.000352526, 0.000105135, 0.0000440287, 0.0000223273, 0.000012822,$
$8.04215 10^{-6}, 5.38984 10^{-6}, 3.80475 10^{-6}, 2.8007 10^{-6}, 2.13405 10^{-6}$
The same happens if x is constant and y increases, or if y is constant and x increases. As long as r increase the difference between the two integrals goes to zero.

Many thanks for your interest. I am grateful.

 

[berkeman]

Unfortunately, I cannot write formulae correctly in this forum

Click on the "LaTeX Guide" link at the lower left of the Edit window. That will show you how to post such equations using LaTeX.

 

[umby]

$\int^{\infty }_0{\frac{e^{-\ \ \frac{1}{2{\varepsilon }^2\ }\left[\frac{{(x-{\varepsilon }^2t)}^2+y^2}{t+1}\right]}}{\sqrt{t}(t+1)}}dt$

Click on the "LaTeX Guide" link at the lower left of the Edit window. That will show you how to post such equations using LaTeX.

View attachment 271275

thank you, it was helpful

 

[berkeman]

thank you, it was helpful

You're very welcome. BTW, using the double-# renders the LaTeX in-line (generally smaller font), and double-$ renders the LaTeX on separate lines, like this:

$$\int^{\infty }_0{\frac{e^{-\ \ \frac{1}{2{\varepsilon }^2\ }\left[\frac{{(x-{\varepsilon }^2t)}^2+y^2}{t+1}\right]}}{\sqrt{t}(t+1)}}dt$$

 

[Office_Shredder]

As x and y go to infinity, the exponential is going to go to zero very fast, so the bulk of the integral is going to be concentrated near t=0. I think the t vs t+1 in the denominators are going to make a huge difference. I would be surprised if they were close to the same value (even in relative terms). Have you plugged it into Wolfram alpha or something to check?

 

[umby]

You are very kind.

$\int_0^{\infty } \frac{\text{Exp}\left[-\frac{1 }{2 \eta ^2} \left(\frac{\left(\xi -\eta ^2 \tau \right)^2+\psi ^2}{(\tau +1)}+\frac{\zeta^2}{\tau }\right)\right]}{\sqrt{\tau } (\tau +1)} \, d\tau$

 

[umby]

As x and y go to infinity, the exponential is going to go to zero very fast, so the bulk of the integral is going to be concentrated near t=0. I think the t vs t+1 in the denominators are going to make a huge difference. I would be surprised if they were close to the same value (even in relative terms). Have you plugged it into Wolfram alpha or something to check?

Thank for your message.
Let's call $f1$ the function:
$\pmb{\text{f1}=\frac{\text{Exp}\left[-\frac{1 }{2 \epsilon ^2} \left(\frac{\left(x-\epsilon ^2 t \right)^2+y^2}{t +1}\right)\right]}{\sqrt{t} (t +1)}}\\$
And $f2$ the function:
$\pmb{\text{f2}=\frac{\text{Exp}\left[-\frac{1 }{2 \epsilon ^2} \left(\frac{\left(x-\epsilon ^2 t \right)^2+y^2}{t }\right)\right]}{\sqrt{t }t }}$

In the figure, plots of $f1$ and $f2$ are reported for increasing values of $x$ and $y$ ($f1$ in blue $f2$ in red).

$f1$ goes to infinity as $t –> 0$ and to 0 as $t->\infty$. Between the two asymptotic branches, $f1$ presents a bump. $f2$ goes to zero both as $t –> 0$ and as $t->\infty$. However, the asymptotic branch of $f1$ close to $t = 0$ becomes less and less important for the integration as $x$ and $y$ increase. At the same time, increasing $x$ and $y$, the bump of $f1$ increases and the two functions get closer and closer. In this conditions, the difference between the two integrals progressively decreases. This is valid for any $\epsilon>0$ and if
$x$ is constant and y increase,
$y$ is constant and x increases,
both $x$ and $y$ increase.
It is possible to demonstrate this?

 

[andrewkirk]

It is possible to demonstrate this?

Yes.

Since we focus on limits as $x,y\to\infty$, we can assume without loss of generality that $\frac x{2\varepsilon^2}>1$. We then note that the integrals from 0 to $\infty$ equal the sum of the integrals over the intervals $(0,1),\ \left(1,\frac x{2\varepsilon^2}\right) ,\ \left(\frac x{2\varepsilon^2}, \frac {3x}{2\varepsilon^2}\right)$ and
$\left(\frac {3x}{2\varepsilon^2}, \infty\right)$.

We show that each of those integrals goes to 0 as $x,y\to\infty$. I have done this and can confirm that it is indeed the case. I won't post my work at present though, as I wouldn't want to spoil the enjoyment of proving it for yourself

Proving that the limit is zero doesn't tell us anything about how rapidly the integrals approach the limit, so I fear even that proof won't assist in estimating error bounds.

 

[umby]

as I wouldn't want to spoil the enjoyment of proving it for yourself

I will enjoy reading your proof anyway, if not more.

 

[Office_Shredder]

I missed that it goes to zero near zero as well.
How similar do you want the integrals to be? If it's just they both go to zero, then they converge to each other the same way they converge to, for example,

$$\int_{0}^{\infty} \frac{1}{x^2+y^2} e^{-t} dt$$.

Or do you care that the relative difference between them goes to zero?

 

[umby]

I missed that it goes to zero near zero as well.
How similar do you want the integrals to be? If it's just they both go to zero, then they converge to each other the same way they converge to, for example,

$$\int_{0}^{\infty} \frac{1}{x^2+y^2} e^{-t} dt$$.

Or do you care that the relative difference between them goes to zero?

Dear Office_Shredder, you are right. Both functions go to zero as $x->0$, or $y->0$, or both go to zero. Then, it is obvious that, under the same condition, their difference goes to zero as well.
Actually, I was looking for a way to solve this integral:
$\int_0^{\infty } \frac{\exp \left(-\frac{\left(x-s^2 t\right)^2+y^2}{(t+1) \left(2 \epsilon ^2\right)}\right)}{\sqrt{t} (t+1)} \, dt$.
And I am interested to find the solution in the limit of $x->0$ and $y->0$. Unfortunately, it seems that this integral cannot be solved symbolically. For this reason, I was looking for a way of approximating the integrand function under these limits. The function
$\frac{\text{Exp}\left[-\frac{1 }{2 \epsilon ^2} \left(\frac{\left(x-\epsilon ^2 t \right)^2+y^2}{t }\right)\right]}{\sqrt{t }t }$,
appeared to be a good candidate for the properties that I have shown. By the way, this function can be symbolically integrated from $0$ to $\infty$. Some time ago, I read about $L_p$ approximation of a function $f1$ as the function $f2$ which satisfies the condition
$\int \left| \text{f1}(t)-\text{f2}(t)\right| ^p \, dt$.
In our case both functions are $>0$, their difference is $>0$, and $p=1$, so that we should have the mean-power approximation. Indeed,
$\int_0^{\infty } \left(\frac{\exp \left(-\frac{\left(x-s^2 t\right)^2+y^2}{(t+1) \left(2 \epsilon ^2\right)}\right)}{\sqrt{t} (t+1)}-\frac{\exp \left(-\frac{\left(x-s^2 t\right)^2+y^2}{t \left(2 \epsilon ^2\right)}\right)}{\sqrt{t} t}\right) \, dt$
goes to zero as $x$ and $y$ $->\infty$.

After your comment I have many doubts however.
Should we look for a function which minimizes the relative difference with the target function?
The relative difference has to be intended as:
$\frac{\left| \text{f1}(t)-\text{f2}(t)\right| }{\text{f1}(t)}$?
Or maybe there is a different solution to the starting problem?