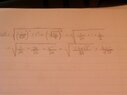Arc Length C: Origin to (6,18,36)

[ineedhelpnow]

let C be the curve of intersection of the parabolic cylinder $x^2=2y$ and the surface $3z=xy$. find the exact length of C from the origin to the point (6,18,36).

please help! this is the last question i have left from this assignment and i have no idea how to do it. i have grading to do and a ton of studying left for my test on monday. i need help now!

 

[MarkFL]

What if you parametrize the curve...can you attempt this?

 

[ineedhelpnow]

ok so i may have exaggerated a bit when i said i have no idea how to do it (Blush)
here's what i did so far. I've been stuck on this for days and i have a feeling i messed up somewhere.
View attachment 3204View attachment 3205

on the second pic that says $\left| r(t) \right|$ on the top right side

 

[MarkFL]

I would try the parametrization:

$$\begin{cases}x(t)=t \\[3pt] y(t)=\dfrac{t^2}{2} \\[3pt] z(t)=\dfrac{t^3}{6} \\ \end{cases}$$

where:

$$0\le t\le6$$

And thus, the arc length $s$ is given by:

$$s=\int_0^6\sqrt{\left(x'(t)\right)^2+\left(y'(t)\right)^2+\left(z'(t)\right)^2}\,dt$$

 

[MarkFL]

I'm going to go ahead and finish this problem...so under the radical in the integrand, we will have:

$$(1)^2+(t)^2+\left(\frac{t^2}{2}\right)^2=\frac{t^4}{4}+t^2+1=\left(\frac{t^2}{2}+1\right)^2$$

Since the quadratic within the parentheses is always positive, our arc-length then becomes:

$$s=\int_0^6\frac{t^2}{2}+1\,dt=\left[\frac{t^3}{6}+t\right]_0^6=6^2+6=6(6+1)=6\cdot7=42$$

 

[ineedhelpnow]

thanks :) i went back to the start of the chapter to start reviewing so i just decided that i would do that problem again once i got to that lesson. thanks for working the whole thing out though. it makes a lot more sense to me that way.