karush
Gold Member
MHB
- 3,240
- 5
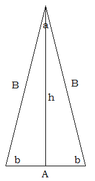
Given an Isosceles triangle with the area of 100 with internal angles of
$$40^o, 70^o,70^o$$
$A=\frac{1}{2}bh$
so
$100=\frac{1}{2}\left(z\sin\left({70^O}\right)\right)\left(2z\cos\left({70^o}\right)\right)$
$z$ is length of one the equal sides
At least started here
$$40^o, 70^o,70^o$$
$A=\frac{1}{2}bh$
so
$100=\frac{1}{2}\left(z\sin\left({70^O}\right)\right)\left(2z\cos\left({70^o}\right)\right)$
$z$ is length of one the equal sides
At least started here
Last edited: