Area moment of inertia calculation without standard formula

[k.udhay]

Hi,

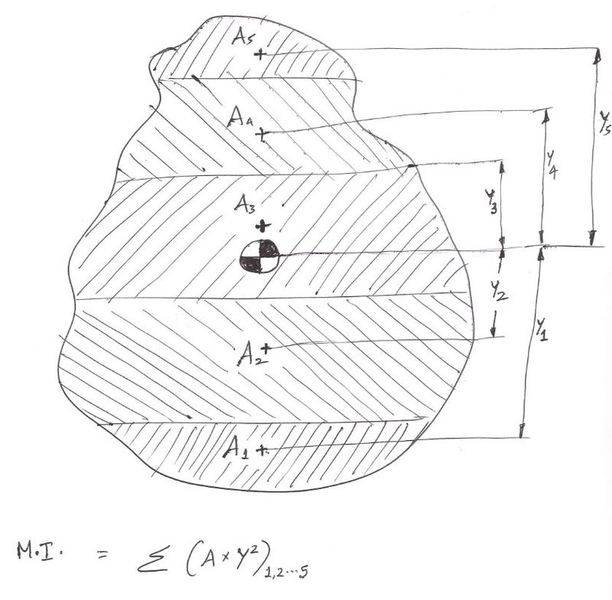
I read in a textbook that area Moment of Inertia (M.I.) of any shape would be Ʃ of (y² χ A)1,2...n where,
A represents the Area of strip no. 1, 2... n
y is the distance between globlal centre of gravity (C.G.) of the shape to th local C.G. of strip no. 1, 2... n
(pl. look at the image)

Though I remember the formula for finding M.I. of a rectangle is [bd³/12] where b and d are breadth and depth of the rectangle, I tried doing it experimentally.

That is:
1. I Drew a rectangle.
2. Split it into 4 equal strips.
3. Measured area and the distance between local and global C.G.s.
4. Did Ʃ of (y²χA)1,2,3 and 4.

I didn't get the value equal to the one done using standard formula. Surprisingly, when I did the same exercise but with splitting the rectangle into 8 equal parts, I got a different answer. But this answer went closer to the M.I. by standard formula.

Now, when I try to find the reason myself, I see that the standard formula has been derived using integration. Since, I am pretty bad in math, can somebody pl. explain me the concept of integration with this example? This will help me to understand when to use integration as well. Many thanks in advance!

 

[tiny-tim]

hi k.udhay!

… Surprisingly, when I did the same exercise but with splitting the rectangle into 8 equal parts, I got a different answer. But this answer went closer to the M.I. by standard formula.

Now, when I try to find the reason myself, I see that the standard formula has been derived using integration. Since, I am pretty bad in math, can somebody pl. explain me the concept of integration with this example? This will help me to understand when to use integration as well. Many thanks in advance!

integration cuts the area into slices

we then pretend that each slice is a perfect rectangle, and we add the moments of inertia for each slice

the more finely we cut the slices, the lower the error is (eg 8 slices is better than 4 )

if we cut it "infinitely" fine, the error tends to zero …

that's integration! ​

 

[k.udhay]

Hi Tim. Thanks for the reply. I understood that the thinner we split it, more accurate the results are. But I want to know how integration does this... I don't know how to put in words. How is integration cutting the rectangle into more thinly strips? Thanks.

 

[tiny-tim]

hi k.udhay!

a completely rigorous proof was known to the ancient greeks …

you slice it into n strips,

then you draw the largest rectangle that just fits inside each strip, and the smallest rectangle that just fits outside

you add up the values for all the inside rectangles, call that sum a_n

and you add up the values for all the outside rectangles, call that sum A_n

obviously the value for the original irregular area is always between a_n and A_n

the difference (A_n - a_n) obviously tends to 0 as n tends to infinity, so both A_n and a_n tend to the same value, A …

so that value, A, must be the value for the original area ​

 

[k.udhay]

Thanks, Tim. I think I will take some more time to completely understand the concept of integration. Though, your explanation has given me a direction to think on. Thanks again!:thumbs:

 

[vlaxk]

Area moment of inertia calc...

MOI can be calculated as ∫y[square]dA...
If we wish to calculate it with respect to horizontal axis of symmetry x...than we need to divide it into infintesimal elements as you were doing...more the divisions, better the solution,less is the error involved...

As per the attachment the infintesimal strip area can be calculated as (b.dy)..
substituting it we get...
I = 2∫y[square] [b.dy]... [limits from 0 to h/2]

solving this you get what you intended to ...
b[d][/3]/12