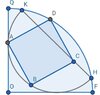
What is the area of square ABCD with OQ = OF = 6?

[maxkor]

Find area of square ABCD if OQ=OF=6.

 

[Opalg]

Here is an outline of a solution using coordinate geometry.

[TIKZ][scale=1.5]
\coordinate [label=above right:{\textcolor{blue}O}] (O) at (0,0) ;
\coordinate [label=above right:{\textcolor{blue}A}] (A) at (0,3.46) ;
\coordinate [label=above right:{\textcolor{blue}B}] (B) at (1.73,0.46) ;
\coordinate [label=above right:{\textcolor{blue}C}] (C) at (4.73,2.19) ;
\coordinate [label=above right:{\textcolor{blue}D}] (D) at (3,5.2) ;
\coordinate [label=above right:{\textcolor{blue}F}] (F) at (6,0) ;
\coordinate [label=above right:{\textcolor{blue}H}] (H) at (5.91,1.02) ;
\coordinate [label=above right:{\textcolor{blue}K}] (K) at (1.02,5.91) ;
\coordinate [label=above right:{\textcolor{blue}Q}] (Q) at (0,6) ;
\coordinate [label=above right:{M}] (M) at (3.46,3.46) ;
\draw [blue, ultra thick] (A) -- (B) -- (C) -- (D) -- cycle ;
\draw [brown, ultra thick] (H) -- (K) ;
\draw [blue, ultra thick] (F) -- (O) -- (Q) ;
\draw [blue, ultra thick] (F) arc (0:90:6) ;
\draw [brown, ultra thick] (K) arc (135:315:3.46) ;
\draw [thin] (A) -- (M) -- (3.46,0) ;
\draw [thin] (K) |- (M) |- (C) ;
\draw (0.9,4.7) node {$s$} ;
\draw (2.2,3.6) node {$s$} ;
\draw (-0.2,1.7) node {$t$} ;
\draw (1.7,-0.2) node {$t$} ;
\draw (3.3,2.8) node {$u$} ;
\draw (4.1,2.1) node {$u$} ;
\draw [thin, dashed] (A) -- (C) ;
\draw [thin, dashed] (B) -- (D) ;
\foreach \point in {O,A,B,C,D,F,H,K,Q} \fill [blue] (\point) circle (2pt) ;
\fill (M) circle (2pt) ;[/TIKZ]
Choose a coordinate system with origin at O, so that F is the point $(6,0)$ and Q is $(0,6)$.

I assume that the brown part of the diagram is meant to be a semicircle and its diameter. Let M be the midpoint of HK, with coordinates $(t,t)$, so that the semicircle has radius $t$. Then the line HK has equation $x+y = 2t$. Let K be the point $(t-s,t+s)$. The distance KM is $t$, from which it follows that $t^2 = 2s^2$. The condition that K lies on the blue circle of radius $6$ is $(t+s)^2 + (t-s)^2 = 36$, from which $3t^2 = 36$ and hence $t = \sqrt{12}$.

Next, let C be the point $(t+u,t-u)$. The centre of the square ABCD is the midpoint of AC, namely $\bigl(\frac12t+ \frac12u, t - \frac12u\bigr)$. You can then calculate that B is the point $\bigl(\frac12t,\frac12t-u\bigr)$ and D is $\bigl(\frac12t + u,\frac32t\bigr)$. The conditions that B lies on the brown semicircle and that D lies on the blue circle both lead to the same equation $2u^2 + 2ut - t^2 = 0$. Therefore $u = \frac12(\sqrt3 - 1)t = 3-\sqrt3$.

Knowing $t$ and $u$, you can then easily check that the distance AB is $t$. So the area of the square ABCD is $t^2 = 12$.

I would much prefer to have a solution using a purely geometric argument, but I do not see how to do that.

 

[maxkor]

Hint:

 

[maxkor]

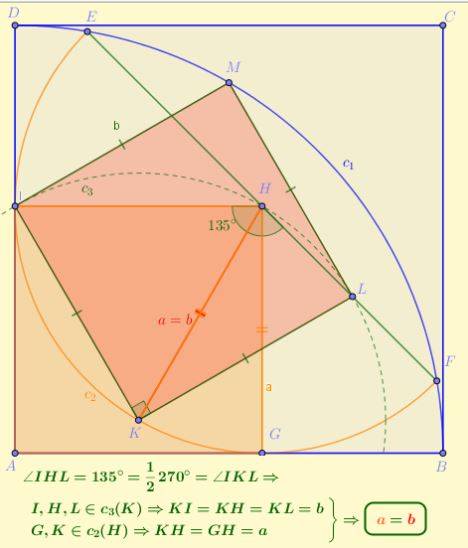
Solution pure geometry: