Area of Triangle ABC Given Dimensions

  • Context: MHB 
  • Thread starter Thread starter maxkor
  • Start date Start date
  • Tags Tags
    Area
Click For Summary

Discussion Overview

The discussion revolves around finding the area of triangle ABC given specific dimensions and angles. Participants explore various methods and reasoning related to the application of geometric principles, particularly the law of cosines.

Discussion Character

  • Homework-related, Mathematical reasoning, Technical explanation

Main Points Raised

  • One participant presents the problem with dimensions and angles for triangle ABC, seeking to find its area.
  • Another participant requests clarification on what the original poster has attempted and where they are experiencing difficulties.
  • A participant shares a diagram but questions the justification for certain elements within it, suggesting there may be alternative methods.
  • Another participant inquires about the method used to derive certain values in the diagram.
  • One participant mentions using Geogebra as a tool for their analysis.
  • A participant states that all sides of triangle AEC are known and applies the law of cosines to derive angles and side lengths, ultimately asserting that the diagram presented is incorrect.

Areas of Agreement / Disagreement

Participants are engaged in a technical discussion with some disagreement regarding the accuracy of the diagram and the methods used to derive certain values. No consensus has been reached on the correct approach or the area of triangle ABC.

Contextual Notes

There are unresolved aspects regarding the assumptions made in the problem setup, the accuracy of the diagram, and the application of the law of cosines. Specific mathematical steps and justifications remain unclear.

maxkor
Messages
79
Reaction score
0
In triangle ABC $AC=BD, CE=2, ED=1, AE=4$ and $\angle CAE=2 \angle DAB$. Find area ABC.
 

Attachments

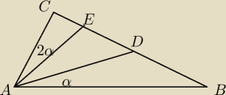
  • 154858.png
    154858.png
    2.1 KB · Views: 135
Mathematics news on Phys.org
Beer induced request follows.
maxkor said:
In triangle ABC $AC=BD, CE=2, ED=1, AE=4$ and $\angle CAE=2 \angle DAB$. Find area ABC.
Please show us what you have tried and exactly where you are stuck.
We can't help you if we don't where you are stuck.
 
This is what it looks like, but how to justify the red ones or maybe there is another way?
 

Attachments

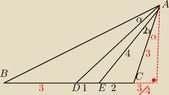
  • 154882.png
    154882.png
    4 KB · Views: 154
How did you get those?
 
Geogebra...
 
In your diagram, all three sides of $\triangle AEC$ are known. Using the law of cosines you get $2\alpha = \cos^{-1}(7/8)$ and $\alpha \approx 14.47751219^{\circ}$.

Continuing to use the law of cosines we get $AD=\dfrac{3\sqrt{10}}{2}$ and $AB=3\sqrt{6}$.

Finally, using the law of cosines on $\triangle ABD$ we get $\alpha \approx 71.170769^{\circ}$.

Your diagram is incorrect.
 

Similar threads

MHB Proving Equality of Angles in an Acute Triangle
  • · Replies 4 ·
Replies
4
Views
1K
MHB Proving $\angle ABC$ is Acute: Inside the Triangle $ABC$
  • · Replies 4 ·
Replies
4
Views
1K
MHB Geom Ch: Prove $AB=x^3$ Given $\triangle ABC$ & $\triangle AEF$
  • · Replies 1 ·
Replies
1
Views
1K
MHB Area of Triangle ABC: Find the Solution
  • · Replies 2 ·
Replies
2
Views
2K
MHB Difference of angles in a triangle
  • · Replies 4 ·
Replies
4
Views
2K
MHB What are the angles of an isosceles triangle with a specific ratio?
  • · Replies 2 ·
Replies
2
Views
1K
MHB Calculating Perimeter & Area of a Parallelogram & Triangle
  • · Replies 1 ·
Replies
1
Views
1K
MHB Can you prove that Triangle $ABC$ is Isosceles?
  • · Replies 1 ·
Replies
1
Views
1K
MHB Can You Solve the Triangle Sides Challenge?
  • · Replies 2 ·
Replies
2
Views
2K
MHB What is the smallest side length BC of triangle ABC with fixed angle and area?
  • · Replies 2 ·
Replies
2
Views
2K