Average acceleration from acceleration vs time graph

[swirly90]

I have a few question regarding Acceleration, I am not sure exactly how to get average acceleration from a acceleration vs. time graph. Do you make a slope? I drew a sample graph, say get the average acceleration from 11s - 25s? Would you try to draw a slope between the two time intervals?

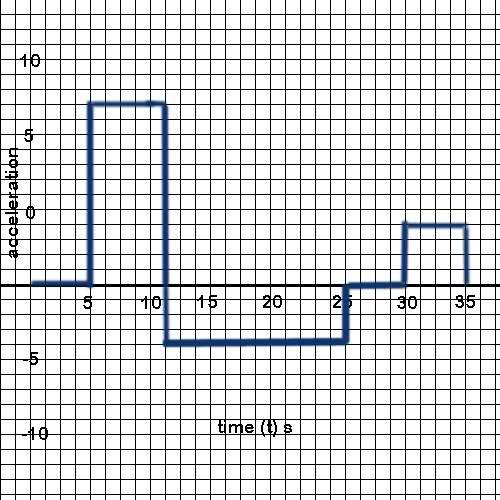
How do you find velocity on a graph like this? Is the area from the line to the zero line?

Thanks for your help.

 

[turin]

(Instantaneous) acceleration is the quotient of some tiny change in velocity divided by the tiny time interval during which the change occurs. Average acceleration is the quotient of some overall change in velocity divided by the overall time interval during which the change occurs. So, if you have this plot of (instantaneous) acceleration in time, the first thing to do is to figure out the overall change in velocity. Then, divid this by the time interval. The change in velocity is the "area under the curve". That is, the change in velocity is the integral of the acceleration over time. If the curve is negative, subtract the area. If the curve is positive, add the area.

 

[kuruman]

The average acceleration can be represented as a rectangle of fixed height on this graph. The base of the rectangle is from zero to 35 s. The height of the rectangle should be such that the area of the rectangle (base*height) is the same as the area under the graph that is given. So the first step is to find the area under the graph above. This would be the sum of two positive and one negative areas.

 

[essecks]

How do you find velocity on a graph like this? Is the area from the line to the zero line?

Without knowing the initial velocity, you can't technically know the velocity of the object. What you CAN know is the overall change in velocity, which as kuruman explained is adding / subtracting the area under the curve depending on whether it's positive/negative.

 

[swirly90]

Thanks, so "under the line" its not velocity but the change in velocity?

 

[essecks]

In some ways, yes - but you don't know where you started initially with the velocity.

In your example graph (assuming the line is zero and each little box is 1 m/s/s high, that scale is a bit off), you'd get:

60 - 48 + 16 = +28 m/s

So you'd be 28 m/s faster than what you started at.

But considering that you could have started at 0 m/s, or 5 m/s, I can't know for sure exactly how fast you're going from that graph, only the overall change.