Average distance between asteroids in the asteroid belt

[ananonanunes]

Homework Statement

Summary: The highest concentration of asteroids is in a doughnut shaped region between the Kirkwood gaps at radii of 2.06AU and 3.27AU from the Sun. There are an estimated 10^9 asteroids of radius 100m or larger. What's the average distance between asteroids?

Relevant Equations

-

What I did was find the total area of the space between the Kirkwood gaps and the area occupied by the asteroids (assuming they all had a 100m radius). I subtracted the two to get the area that is empty in that region. To find the average empty area between asteroids I divided this by the estimated number of asteroids. I don't know how to convert this area into a distance. I tried assuming the area was a square and just finding the lenght of the side or the diagonal of the square, which definetely feels like a big assumption to make, but this results in a much too low number. (The solution is approximately 400 000km)

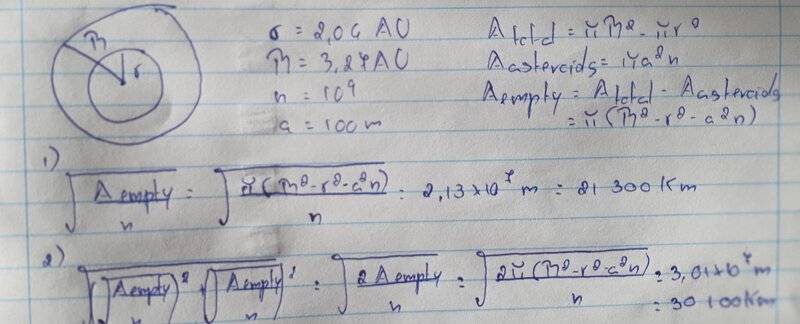
I'm at a loss as to what to do so any help would be appreciated.

 

[jbriggs444]

What I did was find the total area of the space between the Kirkwood gaps

You seem to be assuming that the asteroids are arranged in a flat ring-shaped zone exactly on the plane of the ecliptic. You have calculated the area of this zone.

But the problem describes a volume rather than an area: "The highest concentration of asteroids is in a doughnut shaped region"

I would suggest that you neglect the size of the individual asteroids. The separation between the asteroids is large enough that the distinction between a surface-to-surface measure and a center-to-center measure is irrelevant.

Fine-tuning the calculation to account for the average separation with a random or non-uniform tesselation (or even properly defining the "average separation") would be a rather advanced exercise. Assuming that the asteroids fall into a grid or matrix seems like an eminently reasonable way to proceed.

Consider Googling "crystal structure" for possible three dimensional regular arrangements. But plain old "cubic" is likely what the problem setter has in mind.

 

[ananonanunes]

You seem to be assuming that the asteroids are arranged in a flat ring-shaped zone exactly on the plane of the ecliptic. You have calculated the area of this zone.

But the problem describes a volume rather than an area: "The highest concentration of asteroids is in a doughnut shaped region"

I would suggest that you neglect the size of the individual asteroids. The separation between the asteroids is large enough that the distinction between a surface-to-surface measure and a center-to-center measure is irrelevant.

Fine-tuning the calculation to account for the average separation with a random or non-uniform tesselation (or even properly defining the "average separation") would be a rather advanced exercise. Assuming that the asteroids fall into a grid or matrix seems like an eminently reasonable way to proceed.

Consider Googling "crystal structure" for possible three dimensional regular arrangements. But plain old "cubic" is likely what the problem setter has in mind.

Thank you so much for your help!

 

[Steve4Physics]

In addition to what @jbriggs444 has said, can I add this…

The number of asteroids is only given to the nearest order of magnitude. This implies only an approximate solution is needed. (That's why the official answer is given to only 1 sig. fig.)

I don't know how to convert this area into a distance. I tried assuming the area was a square and just finding the lenght of the side or the diagonal of the square

As already noted by @jbriggs444, you shouldn't be working with areas. But if you were, for this sort of very approximate calculation the side-length of the square would be acceptable - there would be no need to find the length of the diagonal.

Find the volume of the ‘doughnut’ (e.g. imagine it is cut and straightened out to a simple cylinder).

Then find the average volume occupied per asteroid. You should then be able to find the average separation.

 

[ananonanunes]

In addition to what @jbriggs444 has said, can I add this…

The number of asteroids is only given to the nearest order of magnitude. This implies only an approximate solution is needed. (That's why the official answer is given to only 1 sig. fig.)As already noted by @jbriggs444, you shouldn't be working with areas. But if you were, for this sort of very approximate calculation the side-length of the square would be acceptable - there would be no need to find the length of the diagonal.

Find the volume of the ‘doughnut’ (e.g. imagine it is cut and straightened out to a simple cylinder).

Then find the average volume occupied per asteroid. You should then be able to find the average separation.

Thanks for the help!